Question

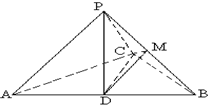如图，已知三棱锥P-ABC中，PA⊥PC，D为AB中点，M为PB的中点，且AB=2PD．
（I）求证：DM∥面PAC；
（II）找出三棱锥P-ABC中一组面与面垂直的位置关系，并给出证明（只需找到一组即可）

Answer 1

分析：（I）根据三角行中位线定理可判得DM∥PA，再根据线面平行判定定理进行求解；
（II）可以找平面PAC⊥平面PBC，然后进行证明，先证明DM⊥PB，再结合（I）条件根据面面垂直的判定定理进行证明；

解答：解：（I）证明：以题意D为AB的中点，M为PB的中点，
∴DM∥PA
又PA?平面PAC，DM?平面PAC
∴DM∥平面PAC；
（II）平面PAC⊥平面PBC
证明：∵AB=2PD，又D为AB的中点
∴PD=BD，又知M为PB的中点
∴DM⊥PB
由（I）知  DM∥PA
∴PA⊥PB，
又由已知PA⊥PC，且PB∩PC=P，
故PA⊥平面PBC，又PA?平面PAC，
∴平面PAC⊥平面PBC；

点评：此题是一道立体几何题，主要考查线面垂直与面面垂直的性质，是一中档题，不是很难，注意第（II）问比较灵活，答案不唯一；