题目内容
1.设a<0,则抛物线y=4ax2的焦点坐标为( )| A. | (a,0) | B. | (-a,0) | C. | $(0,\frac{1}{16a})$ | D. | $(0,-\frac{1}{16a})$ |
分析 化简抛物线方程为标准形式,然后求解焦点坐标即可.
解答 解:a<0,则抛物线y=4ax2的标准方程为:x2=$\frac{1}{4a}y$,焦点坐标在y轴上,焦点坐标为:$(0,\frac{1}{16a})$.
故选:C.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.函数y=ln(2-x-x2)的单调递减区间为( )
| A. | (-∞,-$\frac{1}{2}$] | B. | (-2,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,+∞) | D. | (-$\frac{1}{2}$,1) |
10.曲线y=x4在x=1处的切线方程为( )
| A. | 4x-y-3=0 | B. | x+4y-5=0 | C. | 4x-y+3=0 | D. | x+4y+3=0 |
 如图,在平面直角坐标系xoy中,椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,直线l与x轴交于点E,与椭圆C交于A,B两点.
如图,在平面直角坐标系xoy中,椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,直线l与x轴交于点E,与椭圆C交于A,B两点.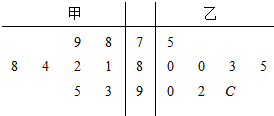 甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示,乙的成绩中有一个数个位数字模糊,在茎叶图中用c表示.(把频率当作概率)
甲、乙两人参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,画出茎叶图如图所示,乙的成绩中有一个数个位数字模糊,在茎叶图中用c表示.(把频率当作概率)