题目内容
已知向量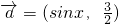 ,
, =(cosx,-1).
=(cosx,-1).
(1)当 时,求cos2x-sin2x的值;
时,求cos2x-sin2x的值;
(2)设x1,x2为函数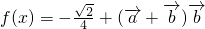 的两个零点,求|x1-x2|的最小值.
的两个零点,求|x1-x2|的最小值.
解:(1)由 得:
得: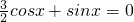 ,
,
若cosx=0,则sinx=±1,不合题意.
则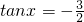 .
.
因此 .
.
(2) =
= =
= =
= .
.
依题得 ,
,
解得 或
或 ,k1,k2∈Z.
,k1,k2∈Z.
又|x1-x2|= ,
,
所以|x1-x2|的最小值为 .
.
分析:(1)根据 ,得到
,得到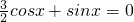 ,确定出tanx的值,化简所求函数,求出其值.
,确定出tanx的值,化简所求函数,求出其值.
(2)利用 =
= =0,确定出两个根,然后再求|x1-x2|及其最小值.
=0,确定出两个根,然后再求|x1-x2|及其最小值.
点评:本题主要是通过向量考查了三角函数,熟练运用向量的知识以及多三角函数进行化简是解决此题的关键.
 得:
得: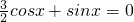 ,
,若cosx=0,则sinx=±1,不合题意.
则
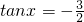 .
.因此
 .
.(2)
 =
= =
= =
= .
.依题得
 ,
,解得
 或
或 ,k1,k2∈Z.
,k1,k2∈Z.又|x1-x2|=
 ,
,所以|x1-x2|的最小值为
 .
.分析:(1)根据
 ,得到
,得到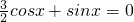 ,确定出tanx的值,化简所求函数,求出其值.
,确定出tanx的值,化简所求函数,求出其值.(2)利用
 =
= =0,确定出两个根,然后再求|x1-x2|及其最小值.
=0,确定出两个根,然后再求|x1-x2|及其最小值.点评:本题主要是通过向量考查了三角函数,熟练运用向量的知识以及多三角函数进行化简是解决此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目