题目内容
【题目】设数列{an}的前项和为Sn ， 若点An（n， 
）在函数f（x）=﹣x+c的图像上运动，其中c是与x无关的常数且a1=3．
（1）求数列{an}的通项公式；
（2）设bn=tanan+1tanan ， tan195+tan3=atan2，求数列{bn}的前99项和（用含a的式子表示）．
【答案】
（1）解：∵点An（n， 
）在函数f（x）=﹣x+c的图像上运动，∴ =﹣n+c，∴Sn=﹣n2+cn，
∵c是与x无关的常数且a1=3．∴3=﹣1+c，解答c=4．
∴Sn=﹣n2+4n．
∴n≥2时，an=Sn﹣Sn﹣1=﹣n2+4n﹣[﹣（n﹣1）2+4（n﹣1）]=﹣2n+5，n=1时也成立
（2）解：∵tan（an+1﹣an）= 
，∴bn=tanan+1tanan= 
﹣1=﹣ 
﹣1．
∴数列{bn}的前99项和T99=﹣ 
+（tana99﹣tana98）+…+（tana2﹣tana1）]﹣99
=﹣ 
﹣99
=a﹣99
【解析】（1）由点An（n， ）在函数f（x）=﹣x+c的图像上运动，可得 =﹣n+c，即Sn=﹣n2+cn，由于c是与x无关的常数且a1=3．代入可得c，再利用递推关系即可得出．（II）由tan（an+1﹣an）= ，可得bn=tanan+1tanan=﹣ ﹣1．即可得出．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系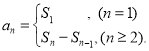
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
练习册系列答案
相关题目
