题目内容
cos2α=
n
n=
cos2α-sin2α
cos2α-sin2α
=1-2sin2α
1-2sin2α
=2cos2α-1
2cos2α-1
.等差数列{an}前n项和Sn=| a1+an |
| 2 |
| a1+an |
| 2 |
na1+
d
| n(n-1) |
| 2 |
na1+
d
.| n(n-1) |
| 2 |
分析:依据二倍角公式和等差数列的前n项和公式.
解答:解:cos2α=cos2α-sin2α=1-2sin2α=2cos2α-1
等差数列前n项和Sn=
n=na1+
d
故答案为:cos2α-sin2α;1-2sin2α;2cos2α-1;
n;na1+
d
等差数列前n项和Sn=
| a1+an |
| 2 |
| n(n-1) |
| 2 |
故答案为:cos2α-sin2α;1-2sin2α;2cos2α-1;
| a1+an |
| 2 |
| n(n-1) |
| 2 |
点评:此题考查了二倍角公式以及等差数列的前n项和公式,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
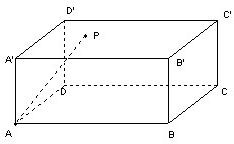 如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )
如图P是长方体AC′上底面内的一点,设AP与三个面A′C′、面A′B、面A′D所成的角为α,β,γ,则cos2α+cos2β+cos2γ=( )| A、1 | ||
| B、2 | ||
C、
| ||
| D、随着P点的位置而定 |