题目内容
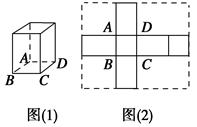
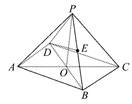
如图,在边长为4的菱形ABCD中,∠DAB=60°,点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
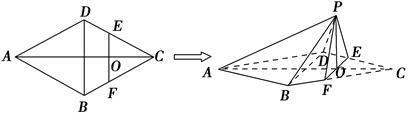
(1)求证:BD⊥平面POA;
(2)记三棱锥PABD体积为V1,四棱锥PBDEF体积为V2,且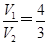 ,求此时线段PO的长.
,求此时线段PO的长.

(1)求证:BD⊥平面POA;
(2)记三棱锥PABD体积为V1,四棱锥PBDEF体积为V2,且
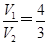 ,求此时线段PO的长.
,求此时线段PO的长.(1)见解析(2)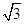
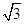
(1)在菱形ABCD中,∵BD⊥AC,
∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF.
∴PO⊥平面ABFED,
∵BD?平面ABFED,
∴PO⊥BD.
∵AO∩PO=O,AO,PO?平面POA.
∴BD⊥平面POA.
(2)设AO∩BD=H
由(1)知,PO⊥平面ABFED,PO=CO.
∴PO是三棱锥PABD的高及四棱锥PBDEF的高
∴V1=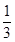 S△ABD·PO,V2=
S△ABD·PO,V2=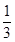 S梯形BFED·PO
S梯形BFED·PO
∵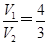 ∴S梯形BFED=
∴S梯形BFED=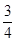 S△ABD=
S△ABD=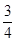 S△BCD
S△BCD
∴S△CEF=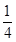 S△BCD
S△BCD
∵BD⊥AC,EF⊥AC,∴EF∥BD,∴△CEF∽△CDB
∴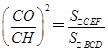 =
=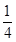
∴CO=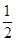 CH=
CH=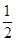 AH=
AH=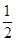 ×2
×2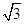 =
=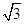
∴线段PO的长为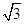 .
.
∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF.
∴PO⊥平面ABFED,
∵BD?平面ABFED,
∴PO⊥BD.
∵AO∩PO=O,AO,PO?平面POA.
∴BD⊥平面POA.
(2)设AO∩BD=H
由(1)知,PO⊥平面ABFED,PO=CO.
∴PO是三棱锥PABD的高及四棱锥PBDEF的高
∴V1=
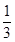 S△ABD·PO,V2=
S△ABD·PO,V2=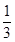 S梯形BFED·PO
S梯形BFED·PO∵
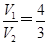 ∴S梯形BFED=
∴S梯形BFED=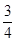 S△ABD=
S△ABD=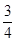 S△BCD
S△BCD∴S△CEF=
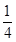 S△BCD
S△BCD∵BD⊥AC,EF⊥AC,∴EF∥BD,∴△CEF∽△CDB
∴
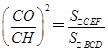 =
=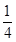
∴CO=
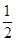 CH=
CH=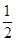 AH=
AH=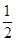 ×2
×2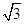 =
=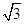
∴线段PO的长为
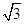 .
.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
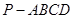 中,
中,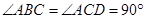 ,
, ,
, ,
, 为
为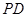 的中点,
的中点, 为
为 的中点,
的中点,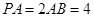 .
.
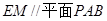 ;
;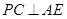 ;
;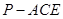 的体积
的体积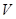 .
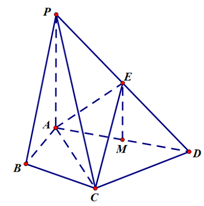
.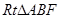 中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.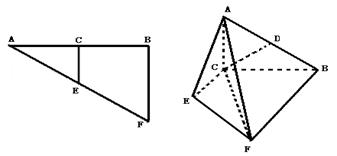
 中,
中, 且
且 .
.
 ;
; .
.
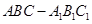 中,
中,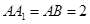 ,
,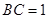 ,
,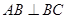 ,则该三棱柱的侧面积为 .
,则该三棱柱的侧面积为 .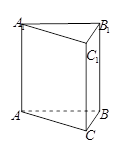
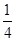 ,则此长方体的体积是________.
,则此长方体的体积是________.