题目内容
已知函数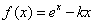 ,.
,.
(Ⅰ)若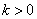 ,且对于任意
,且对于任意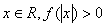 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅱ)设函数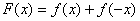 ,求证:
,求证:
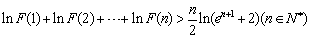
解:(Ⅰ)由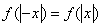 可知
可知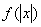 是偶函数.
是偶函数.
于是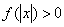 对任意
对任意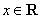 成立等价于
成立等价于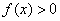 对任意
对任意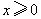 成立.
成立.
由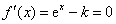 得
得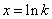 .
.
①当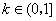 时,
时,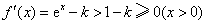 .
.
此时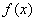 在
在 上单调递增. 故
上单调递增. 故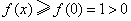 ,符合题意.
,符合题意.
②当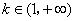 时,
时,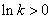 .
.
当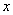 变化时
变化时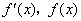 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递减 | 极小值 | 单调递增 |
由此可得,在 上,
上,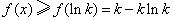 .
.
依题意,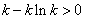 ,又
,又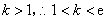 .
.
综合①,②得,实数 的取值范围是
的取值范围是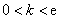 .
.
(Ⅱ)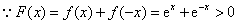 ,
,

又
 ,
,
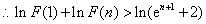 ,
,

由此得:
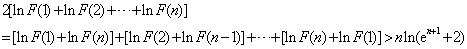
故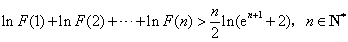 成立.
成立.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
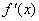

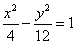
 的左焦点,
的左焦点,
 是双曲线右支上的动点,则
是双曲线右支上的动点,则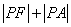
 的最小值为 .
的最小值为 . ,若
,若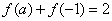 ,则实数
,则实数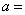 .
.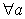 、
、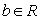 ,运算“
,运算“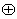 ”、“
”、“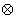 ”定义为:
”定义为: =
=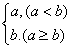 ,
,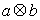 =
=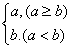 ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( )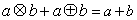 ⑵
⑵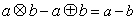
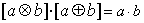 ⑷
⑷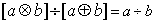
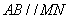 ,且
,且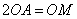 ,若
,若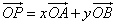 ,
,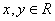 ),则终点
),则终点 落在阴影部分(含边界)
落在阴影部分(含边界) 的取值范围是 .
的取值范围是 . 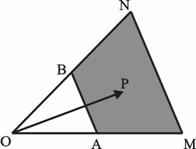
 样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若
样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若 样本数据恰好是
样本数据恰好是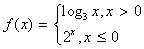 ,则
,则 .
.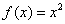 B、
B、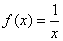 C、
C、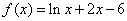 D、
D、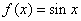
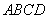 中,
中,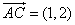 ,
,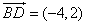 ,则该平面四边形的面积为
,则该平面四边形的面积为 B.
B.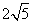 C.5 D.10
C.5 D.10