题目内容
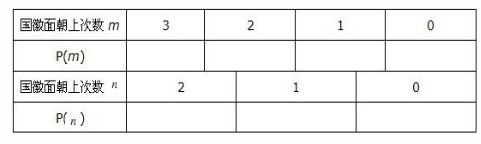
甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为m;乙用一枚硬币掷2次,记正面朝上的次数为n.(1)填表:
m | 3 | 2 | 1 | 0 |
P(m) |
|
|
|
|
n | 2 | 1 | 0 |
P(n) |
|
|
|
(2)现规定:若m＞n,则甲胜;若n≥m,则乙胜.你认为这种规定合理吗?为什么?
解：(1)
m | 3 | 2 | 1 | 0 |
P(m) |
|
|
|
|
n | 2 | 1 | 0 |
P(n) |
|
|
|
(2)m＞n时,甲胜的概率为P(m＞n)=
+
(
+
)+
×
=
.同理,n≥m时,乙胜的概率为P(n≥m)=
.
故P(m＞n)=P(n≥m),即甲胜与乙胜的机会是均等的,从而此种规定公平合理.
练习册系列答案
阅读快车系列答案
相关题目
甲与乙两人掷硬币，甲用一枚硬币掷3次，记下国徽面（记为正面）朝上的次数为m；乙用一枚硬币掷2次，记下国徽面（记为正面）朝上的次数为n．
（1）填写下列两表：
正面向上次数m | 3 | 2 | 1 | 0 |
概率P（m） |
|
|
|
|
正面向上次数n | 2 | 1 | 0 |
概率P（n） |
|
|
|
（2）若规定m ＞n时，甲胜．求甲获胜的概率．
；乙用这枚硬币掷2次，记正面朝上的次数为
。
，则甲获胜；若
，则乙获胜，分别求出甲和乙获胜的概率.
、
．假设每次射击是否击中目标相互之间没有影响，两人射击是否击中目标相互之间也没有影响．