Question

甲与乙两人掷硬币，甲用一枚硬币掷3次，记下国徽面朝上的次数为m；乙用一枚硬币掷2次，记下国徽面朝上的次数为n．
（1）算国徽面朝上不同次数的概率并填入下表：
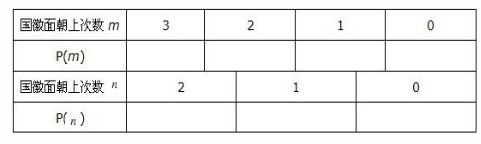
（2）现规定：若m＞n，则甲胜；若n≥m，则乙胜．你认为这种规定合理吗？为什么？

Answer 1

分析：首先分析题目对于（1）可直接根据相互独立事件概率乘法公式求得每个事件的概率填入表格即可．
对于（2）可根据（1）求得的数据，分别求出若m＞n甲胜的概率和n≥m乙胜的概率．判断它们的概率是否都相等且等于

1

2

，即判断甲乙获胜的概率是否相等，即可判断规定是否合理．

解答：解：（1）根据相互独立事件概率乘法公式得：

（2）这种规定是合理的．这是因为甲获胜，则m＞n
当m=3时，n=2，1，0，其概率为

1

8

×(

1

4

+

1

2

+

1

4

)=

1

8

当m=2时，n=1，0，其概率为

3

8

×(

1

2

+

1

4

)=

9

32

；
当m=1时，n=0，其概率为

3

8

×

1

4

=

3

32

；
∴甲获胜的概率为

1

8

+

9

32

+

3

32

=

1

2

若乙获胜，则m≤n
当n=2时，m=2，1，0，其概率为

1

4

×(

3

8

+

3

8

+

1

8

)=

7

32

；
当n=1时，m=1，0，其概率为

1

2

×(

3

8

+

1

8

)=

8

32

；
当n=0时，m=0，其概率为

1

4

×

1

8

=

1

32

；
∴乙获胜的概率为

7

32

+

8

32

+

1

32

=

1

2

甲和乙获胜的概率老都是，即获胜机会相等，所以这种规定是合理的．

点评：此题最主要考查超几何分布的概率的求法，其中涉及到判断规定是否合理的问题，即实际应用问题．这类题型体现了新课程的要求，在高考中多次出现，希望同学们要多加注意．