题目内容
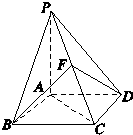
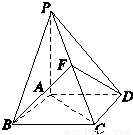
如图,已知点P为菱形ABCD所在平面外一点,并且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.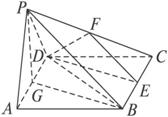
(1)求证:AD⊥PB;
(2)求二面角A-BC-P的大小;
(3)设E为BC边的中点,F为PC中点,求证:平面DEF⊥平面ABCD.
(1)证明:取AD中点G,连结PG.

∵△PAD为等边三角形,
∴PG⊥AD.
又由已知平面PAD⊥平面ABCD.
∴PG⊥平面ABCD.
连结BG,BG是PB在平面ABCD上的射影.
由于四边形ABCD是菱形,∠DAB=60°,
∴△ABD,△BCD均为等边三角形.
∴BG⊥AD.∴AD⊥PB.
(2)解:∵AD∥BC,∴BG⊥BC,PB⊥BC.
∴∠PBG是二面角ABCP的平面角.
又PG、BG分别是两个边长相等的等边三角形的高.
∴PG=BG.∴∠PBG=45°,
即二面角ABCP的平面角为45°.
(3)证明:∵DE是等边三角形BCD的中线,
∴BC⊥DE.
∵E、F分别是BC、PC中点,∴EF∥BP.
∴BC⊥EF.∴BC⊥平面DEF.
∴平面DEF⊥平面ABCD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
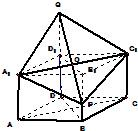 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1>
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1> 如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )
如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )