题目内容
【题目】已知函数f（x）=x2+ax+b﹣a（a，b∈R）．
（1）若关于x的不等式f（x）＞0的解集为（﹣∞，﹣1）∪（3，+∞），求实数a，b的值；
（2）设a=2，若不等式f（x）＞b2﹣3b对任意实数x都成立，求实数b的取值范围；
（3）设b=3，解关于x的不等式组 
．
【答案】
（1）解：因为不等式f（x）=x2+ax+b﹣a＞0的解集为（﹣∞，﹣1）∪（3，+∞），
所以由题意得﹣1，3为函数x2+ax+b﹣a=0的两个根，
所以 
，解得a=﹣2，b=﹣5
（2）解：当a=2时，x2+2x+b﹣2＞b2﹣3b恒成立，即x2+2x﹣2＞b2﹣4b恒成立．
因为x2+2x﹣2=（x+1）2﹣3≥﹣3，所以b2﹣4b＜﹣3，
解之得1＜b＜3，所以实数b的取值范围为1＜b＜3
（3）当b=3时，f（x）=x2+ax+3﹣a，f（x）的图象的对称轴为 
．
（ⅰ）当△＜0，即﹣6＜a＜2时，由 
，得x＞1，
（ⅱ）当△=0，即a=2或﹣6时
①当a=2时，由 ，得 
，所以x＞1，
②当a=﹣6时，由 ，得 
，所以1＜x＜3或x＞3，
（ⅲ）当△＞0，即a＜﹣6或a＞2时，方程f（x）=0的两个根为 
， 
，
①当a＜﹣6时，由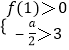 
知1＜x1＜x2，所以 的解为1＜x＜x1或x＞x2，
②当a＞2时，由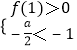 
知x1＜x2＜1，所以 的解为x＞1，
综上所述，
当a≤﹣6时，不等式组的解集为 
，
当a＞﹣6时，不等式组的解集为（1，+∞）
【解析】（1）把问题转化为一元二次方程的问题，利用方程的根建立二次一次方程组，求得a和b的值．（2）把不等式整理成x2+2x﹣2＞b2﹣4b确定等号左边的最小值，进而确定等号右边的范围求得b的范围．（3）对判别式△大于0和小于0进行分类讨论，通过解不等式求得解集．
【考点精析】认真审题，首先需要了解二次函数的性质(当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减)．
