题目内容
18.在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N,若向量$\overrightarrow{OM}$=sinθ•$\overrightarrow{OA}$,向量$\overrightarrow{ON}$=cosθ•$\overrightarrow{OB}$,其中,θ∈(0,$\frac{π}{2}$).(1)求sin2θ的值;
(2)记△OMN的面积为S1,平行四边形OABC的面积为S,试求$\frac{{S}_{1}}{S}$的值.
分析 (1)根据条件、向量加法的几何意义及相等向量便可得到$\overrightarrow{ON}=cosθ•\overrightarrow{OC}+\frac{cosθ}{sinθ}•\overrightarrow{OM}$,而根据C,N,M三点共线,便有$cosθ+\frac{cosθ}{sinθ}=1$,这样便可解出$sinθcosθ=\sqrt{2}-1$,从而得出sin2θ=$2\sqrt{2}-2$;
(2)根据条件可得到OM•ON=sinθcosθ•OA•OB,然后根据三角形的面积公式便可得出2S1=sinθcosθ•S,带入上面求出的sinθcosθ即可得出$\frac{{S}_{1}}{S}$.
解答 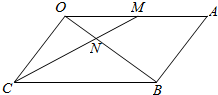 解:(1)如图:
解:(1)如图:
$\overrightarrow{ON}=cosθ•\overrightarrow{OB}$=$cosθ•(\overrightarrow{OC}+\overrightarrow{OA})$=$cosθ•\overrightarrow{OC}+\frac{cosθ}{sinθ}•sinθ•\overrightarrow{OA}$=$cosθ•\overrightarrow{OC}+\frac{cosθ}{sinθ}•\overrightarrow{OM}$;
∵C,N,M三点共线;
∴$cosθ+\frac{cosθ}{sinθ}=1$;
∴sinθcosθ=sinθ-cosθ;
∴(sinθcosθ)2+2sinθcosθ-1=0;
∵$θ∈(0,\frac{π}{2})$;
∴$sinθcosθ=\frac{-2+\sqrt{8}}{2}=-1+\sqrt{2}$;
∴$sin2θ=2\sqrt{2}-2$;
(2)∵$\overrightarrow{OM}=sinθ•\overrightarrow{OA},\overrightarrow{ON}=cosθ•\overrightarrow{OB}$,sinθ>0,cosθ>0;
∴OM=sinθ•OA,ON=cosθ•OB;
∴OM•ON=sinθcosθ•OA•OB;
∴OM•ONsin∠MON=sinθcosθ•OA•OB•sin∠MON;
∴2S1=sinθcosθ•S;
∴$\frac{{S}_{1}}{S}=\frac{sinθcosθ}{2}=\frac{\sqrt{2}-1}{2}$.
点评 考查向量加法的几何意义,向量的数乘运算,相等向量的概念,以及三点A,B,C共线时$\overrightarrow{OB}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$,则有λ+μ=1,向量数乘的几何意义,三角形的面积公式,二倍角的正弦公式.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(1)请将上表补充完整(不用写计算过程);
(2)请问有多大的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$+3 | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
(I)当a=2时,求曲线y=f(x)在点(1,f(1))处切线的斜率;
(II)当a=3时,求函数f(x)的单调区间.
①命题“p∧q”为真;
②命题“p∧?q”为假;
②命题“¬p∨q”为真;
④命题“¬p∨¬q”为假;
其中正确的命题序号为( )
| A. | ②④ | B. | ②③ | C. | ③④ | D. | ①②③ |
| A. | 0 | B. | 2 | C. | 5 | D. | 10 |