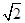题目内容
设 ,点
,点 为
为 所表示的平面区域内任意一点,
所表示的平面区域内任意一点, ,
, 为坐标原点,
为坐标原点, 为
为 的最小值,则
的最小值,则 的最大值为
的最大值为
A. | B. | C. | D. |
A
解析试题分析:由题意, f(x)=(0,-5)•(x,y)=-5y,当y取最大值时,f(x)取最小值f(m), 所表示的平面区域如图所示
所表示的平面区域如图所示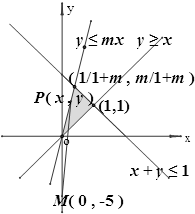
由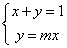 ,可得y=
,可得y=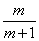 ,所以f(m)=-5×
,所以f(m)=-5×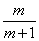 =-5(1-
=-5(1-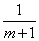 )=-5+
)=-5+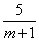 ,
,
由于m≥2,所以当m=2时,f(m)max= ,故选A.
,故选A.
考点:本题主要考查平面向量的坐标运算,数量积,简单线性规划。
点评:中档题,本题具有一定综合性,较之于一般的简单线性规划问题略为复杂,主要是平面区域的“不确定性”。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
平面向量 与
与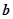 的夹角为60°,
的夹角为60°, 则
则 ( )
( )
A. | B. | C.4 | D.12 |
在 中,
中, ,如果不等式
,如果不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.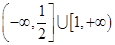 | D. |
已知向量 不共线,
不共线, 如果
如果 //
// 那么 ( )
那么 ( )
A. 且c与d反向 且c与d反向 | B. 且c与d反向 且c与d反向 |
C. 且c与d同向 且c与d同向 | D. 且c与d同向 且c与d同向 |
已知点 ,
, ,则与
,则与 共线的单位向量为( )
共线的单位向量为( )
A. 或 或 | B. |
C. 或 或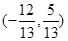 | D. |
点O是 ABC所在平面内一定点,动点P满足
ABC所在平面内一定点,动点P满足 ,则动点P的轨迹一定通过三角形ABC的( )
,则动点P的轨迹一定通过三角形ABC的( )
| A.重心 | B.垂心 | C.外心 | D.内心 |
矩阵A ,向量
,向量 ,则A
,则A
 ( )
( )
A. | B. | C. | D. |
平面向量的集合 到
到 的映射
的映射 由
由 确定,其中
确定,其中 为常向量.若映射
为常向量.若映射 满足
满足 对
对 恒成立,则
恒成立,则 的坐标不可能是 ( )
的坐标不可能是 ( )
A. | B. |
C. | D. |
 、
、 、
、 满足
满足 ,
, ,
,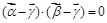 .若对每一确定的
.若对每一确定的 ,
, 的最大值和最小值分别为
的最大值和最小值分别为 、
、 ,则对任意
,则对任意 的最小值是 ( )
的最小值是 ( )