题目内容
17.已知三角形的三个顶点坐标为A(-3,1),B(3,-3),C(1,7).证明△ABC为等腰直角三角形.分析 利用A(-3,1),B(3,-3),C(1,7),可得$\overrightarrow{AC}$=(-4,6),$\overrightarrow{AB}$=(6,-4),证明|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$|,$\overrightarrow{AC}$•$\overrightarrow{AB}$=0,即可得出结论.
解答 证明:∵A(-3,1),B(3,-3),C(1,7),
∴$\overrightarrow{AC}$=(-4,6),$\overrightarrow{AB}$=(6,-4),
∴|$\overrightarrow{AC}$|=|$\overrightarrow{AB}$|,$\overrightarrow{AC}$•$\overrightarrow{AB}$=0,
∴△ABC为等腰直角三角形.
点评 本题考查证明△ABC为等腰直角三角形,正确运用向量知识是关键.

练习册系列答案
相关题目
7.某商品在5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是$\stackrel{∧}{y}$=-3.2x+4a,则a=10.
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
12.已知双曲线的渐近线方程为y=±$\sqrt{2}$x,焦点坐标为(-$\sqrt{6}$,0),($\sqrt{6}$,0),则双曲线方程为( )
| A. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{8}$=1 | B. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 |
2.已知二次函数y=ax2+2bx的图象如图所示,则$\root{4}{(a-b)^{4}}$的值为( )
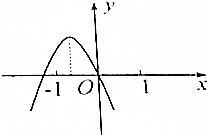

| A. | a+b | B. | -(a+b) | C. | a-b | D. | b-a |