题目内容
求出下列函数的值域:
y=2x+4
;
y=
.
y=2x+4
| 1-x |
y=
| 2x2-3 |
| x2+1 |
分析:对于第一个函数,先求出它的定义域,换元后化为关于t的二次函数,利用二次函数的性质以及t的范围求出它的值域.
对于第二个函数,由其解析式可得x2=
≥0,解此分使不等式,求得y的范围,即为函数的值域.
对于第二个函数,由其解析式可得x2=
| 3+y |
| 2-y |
解答:解:∵y=2x+4
,故函数的定义域为(-∞,1].
令
=t,可得 x=1-t2≤1,此时t≥0,函数y=2(1-t2)+4t=4-2(t-1)2≤4,
故函数y=2x+4
的值域为(-∞,4].
由函数y=
可得 x2=
≥0,即
≤0,即
,
解得-3≤y<2,故函数y=
的值域为[-3,2).
| 1-x |
令
| 1-x |
故函数y=2x+4
| 1-x |
由函数y=
| 2x2-3 |
| x2+1 |
| 3+y |
| 2-y |
| y+3 |
| y-2 |
|
解得-3≤y<2,故函数y=
| 2x2-3 |
| x2+1 |
点评:本题主要考查函数的定义域和值域的求法,分式不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设
设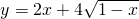 ;
; .
.