题目内容
已知点
是函数
(a＞0，且a≠1)的图像上一点.等比数列{an}的前n项和为f(n)－c．数列{bn}(bn＞0)的首项为c，且前n项和Sn满足
．
⑴求数列{an}和{bn}的通项公式；
⑵若数列
的前n项和为Tn，问满足
的最小正整数n是多少？
（本题满分12分）
解：⑴
，∴
1分
，
，
．
又数列{an}成等比数列，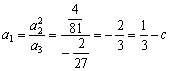
，所以c＝1；
又公比
，所以
4分
又bn＞0，
＞0，∴
；
数列
构成一个首相为1公差为1的等差数列，
，
Sn＝n2，当n≥2，bn＝Sn－Sn－1＝n2－(n－1)2＝2n－1；
∴bn＝2n－1(n∈N*) 8分
＝
＝
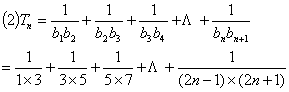
由
得n＞90
满足
的最小正整数为91 12分
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
是函数
(a＞0，且a≠1)的图像上一点.等比数列{an}的前n项和为f(n)－c．数列{bn}(bn＞0)的首项为c，且前n项和Sn满足
．
的前n项和为Tn，问满足
的最小正整数n是多少？
是函数f（x）=ax（a＞0，且a≠1）的图象上一点．等比数列{an}的前n项和为f（n）-1．数列{bn}（bn＞0）的首项为1，且前n项和sn满足
的前n项和为Tn，问满足Tn＞
的最小正整数n是多少？
是函数f（x）=ax（a＞0，且a≠1）的图象上一点．等比数列{an}的前n项和为f（n）-1．数列{bn}（bn＞0）的首项为1，且前n项和sn满足
的前n项和为Tn，问满足Tn＞
的最小正整数n是多少？
是函数y=2x的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论
成立．运用类比思想方法可知，若点A（x1，sin1）、B（x2，sinx2）是函数y=sinx（x∈（0，π））的图象上的不同两点，则类似地有 成立．