题目内容
若直线ax+2by-2=0(a,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则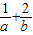 的最小值为 .
的最小值为 .
【答案】分析:由题意可知圆x2+y2-4x-2y-8=0的圆心(2,1)在直线ax+2by-2=0上,可得a+b=1,而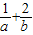 =(
=(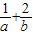 )(a+b),展开利用基本不等式可求最小值
)(a+b),展开利用基本不等式可求最小值
解答:解:由圆的性质可知,直线ax+2by-2=0即是圆的直径所在的直线方程
∵圆x2+y2-4x-2y-8=0的标准方程为(x-2)2+(y-1)2=13,
∴圆心(2,1)在直线ax+2by-2=0上
∴2a+2b-2=0即a+b=1
∵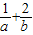 =(
=(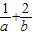 )(a+b)=
)(a+b)=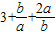
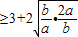 =3+2
=3+2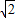
∴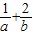 的最小值
的最小值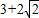
故答案为: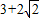
点评:本题主要考查了圆的性质的应用,利用基本不等式求解最值的问题,解题的关键技巧在于“1”的基本代换
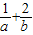 =(
=(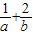 )(a+b),展开利用基本不等式可求最小值
)(a+b),展开利用基本不等式可求最小值解答:解:由圆的性质可知,直线ax+2by-2=0即是圆的直径所在的直线方程
∵圆x2+y2-4x-2y-8=0的标准方程为(x-2)2+(y-1)2=13,
∴圆心(2,1)在直线ax+2by-2=0上
∴2a+2b-2=0即a+b=1
∵
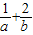 =(
=(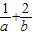 )(a+b)=
)(a+b)=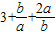
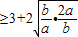 =3+2
=3+2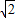
∴
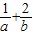 的最小值
的最小值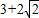
故答案为:
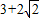
点评:本题主要考查了圆的性质的应用,利用基本不等式求解最值的问题,解题的关键技巧在于“1”的基本代换

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
若直线ax+2by-2=0(a,b∈(0,+∞)平分圆x2+y2-4x-2y-6=0,则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
| C、2 | ||
| D、5 |
若直线ax+2by-2=0(a>0,b>0)始终平分圆x2+y2-4x-2y-8=0的周长,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
| A、1 | ||
B、3+2
| ||
| C、5 | ||
D、4
|