题目内容
18．i+i2+i3+…+i2017=i．分析 利用复数的周期性、等比数列的求和公式即可得出．
解答 解：∵i4=1，
∴原式=$\frac{i（1-{i}^{2017}）}{1-i}$=$\frac{i（1-i）}{1-i}$=i．
故答案为：i．
点评 本题考查了复数的运算法则、周期性、等比数列的求和公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
8．已知集合A={x|$\frac{x-1}{x+2}$≤0}，B={x|x＜-2}，则A∪（∁UB）=（ ）
| A． | [-2，+∞） | B． | （-2，+∞） | C． | [-2，1] | D． | （-2，1] |
9．已知正项等比数列{an}满足：a7=a6+2a5，若存在两项am、an使得$\sqrt{{a}_{m}{a}_{n}}$=4a1，则$\frac{1}{m}$+$\frac{4}{n}$的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{5}{3}$ | C． | $\frac{25}{6}$ | D． | $\frac{4}{3}$ |
6．下列求导运算正确的是（ ）
| A． | （log2x）′=$\frac{1}{xln2}$ | B． | （$\frac{cosx}{x}$）′=$\frac{xsinx-cosx}{x}$ | ||
| C． | （10x）′=10xlge | D． | （x+$\sqrt{x}$）′=1-$\frac{1}{2\sqrt{x}}$ |
13．如图所示给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图，其中判断框内应填入的条件是（ ）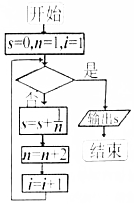
| A． | i＞1010 | B． | i＜1010 | C． | i＞1009 | D． | i＜1009 |
3．△ABC的内角A，B，C所对的边分别为a，b，c，a2+b2-c2=6$\sqrt{3}$-2ab，且C=60°，则△ABC的面积为（ ）
| A． | 2 | B． | $\frac{3}{2}$ | C． | $\frac{4}{3}$ | D． | $\frac{5}{3}$ |
10．某数学兴趣小组有3名男生和2名女生，从中任选出2名同学参加数学竞赛，那么对立的两个事件为（ ）
| A． | 恰有1名女生与恰有2名女生 | B． | 至少有1名男生与全是男生 | ||
| C． | 至少有1名男生与至少有1名女生 | D． | 至少有1名女生与全是男生 |
7．若复数z=$\frac{3+ai}{2-i}$（a∈R，i是虚数单位）是纯虚数，则复数z的共轭复数是（ ）
| A． | $\frac{9}{5}$i | B． | -$\frac{9}{5}$i | C． | 3i | D． | -3i |