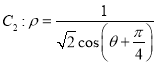题目内容
【题目】已知函数![]() 存在唯一的极值点
存在唯一的极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)求导得到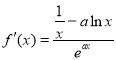 ,设
,设![]() ,讨论
,讨论![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,根据零点存在定理计算得到答案.
四种情况,根据零点存在定理计算得到答案.
(2)根据题意得到![]() ,
,![]() ,根据
,根据![]() 得到
得到![]() ,化简得到答案.
,化简得到答案.
(1)函数的定义域为![]() ,
,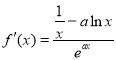 ,令
,令![]() ,
,
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递增,不合题意;
上单调递增,不合题意;
②若![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
(ⅰ)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,不合题意;
上单调递增,不合题意;
(ⅱ)若![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
因为![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上有两个变号零点,所以
上有两个变号零点,所以![]() 有两个极值点,不合题意;
有两个极值点,不合题意;
③若![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
且![]() ,
,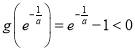 ,存在唯一
,存在唯一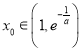 ,使
,使![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 是
是![]() 的唯一极值点,符合题意;
的唯一极值点,符合题意;
综上,![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)可知,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
由(1)可知函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
现证明不等式:![]() ,其中
,其中![]()
要证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
即证![]() ,易知成立.
,易知成立.
所以![]() ,即
,即![]() ,
,
即![]() ,所以
,所以![]() ,证毕.
,证毕.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
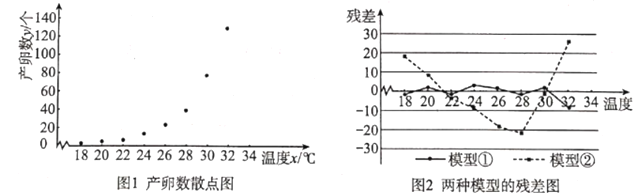
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为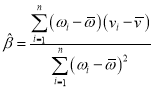 ,
,![]() .
.