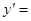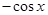题目内容
已知函数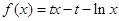
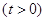 .
.
(Ⅰ)若函数 在
在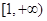 上为增函数,求实数
上为增函数,求实数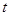 的取值范围;
的取值范围;
(Ⅱ)当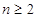 且
且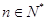 时,证明:
时,证明: 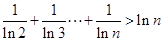 .
.
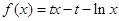
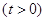 .
.(Ⅰ)若函数
 在
在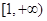 上为增函数,求实数
上为增函数,求实数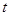 的取值范围;
的取值范围;(Ⅱ)当
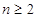 且
且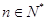 时,证明:
时,证明: 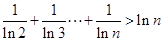 .
.(I)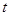 的取值范围为
的取值范围为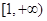 .(Ⅱ)详见解析.
.(Ⅱ)详见解析.
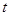 的取值范围为
的取值范围为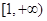 .(Ⅱ)详见解析.
.(Ⅱ)详见解析.试题分析:(I)函数
 在
在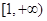 上为增函数,则导数
上为增函数,则导数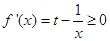 在
在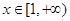 上恒成立,即
上恒成立,即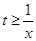 在
在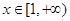 上恒成立.这只需
上恒成立.这只需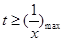 即可.(Ⅱ)注意用第(I)题的结果.由(I)可得,
即可.(Ⅱ)注意用第(I)题的结果.由(I)可得, 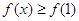 ,从而得
,从而得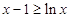 恒成立,(当且仅当
恒成立,(当且仅当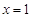 时,等号成立),由此得
时,等号成立),由此得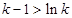 ,即
,即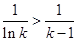 .如何将这个这个不等式与待证不等式联系起来?在
.如何将这个这个不等式与待证不等式联系起来?在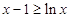 中,令
中,令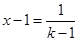 ,得
,得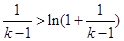 .
.由此得
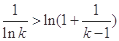 ,即
,即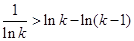 .这样叠加即可得:
.这样叠加即可得: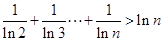 .
.试题解析:(I)函数
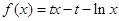 的定义域为
的定义域为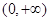 . 1分
. 1分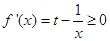 在
在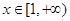 上恒成立,即
上恒成立,即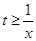 在
在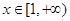 上恒成立, 2分
上恒成立, 2分∵
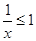 ∴
∴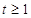 ,∴
,∴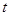 的取值范围为
的取值范围为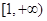 4分
4分(Ⅱ)由(I)当
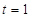 ,
,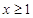 时,
时,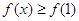 ,又
,又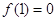 ,
,∴
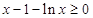 (当
(当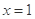 时,等号成立),即
时,等号成立),即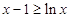 5分
5分又当
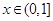 时,设
时,设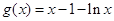 ,
, 则
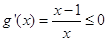 ∴
∴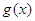 在
在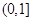 上递减,
上递减,∴
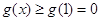 ,即
,即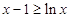 在
在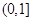 恒成立,
恒成立, ∴
 时,
时,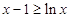 ①恒成立,(当且仅当
①恒成立,(当且仅当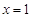 时,等号成立), 7分
时,等号成立), 7分∴当
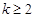 时,
时,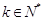 ,由①得
,由①得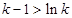 ,即
,即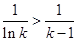 ..②.
..②.当
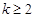 时,
时,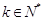 ,
,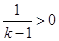 ,在
,在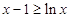 中,令
中,令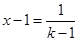 ,得
,得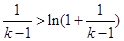 .. ③.
.. ③.∴由②③得,当
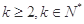 时,
时,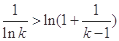 ,即
,即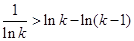 . 10分
. 10分∴
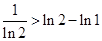 ,
,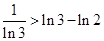 ,
, 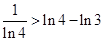 ,
,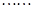
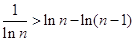 .
.∴
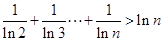 . 12分
. 12分
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
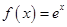 .
.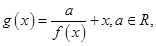 求
求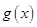 的极值.
的极值.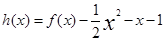 在
在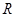 上为增函数。
上为增函数。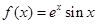 函数.
函数.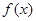 单调递增区间;
单调递增区间;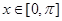 时,求函数
时,求函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
. 的单调区间;
的单调区间; 时,求函数
时,求函数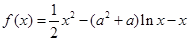 .
.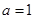 ,求曲线
,求曲线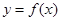 在点
在点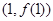 处的切线方程;
处的切线方程; 的单调性.
的单调性.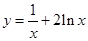 的单调减区间为___________.
的单调减区间为___________.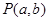 在函数
在函数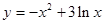 的图像上,点
的图像上,点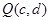 在函数
在函数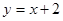 的图像上,则
的图像上,则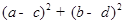 的最小值为( )
的最小值为( )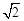
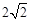
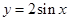 的导数
的导数