题目内容
5.在△ABC中,sinA:sinB:sinC=1:1:$\sqrt{2}$,且△ABC的面积为$\frac{1}{2}$,则$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$的值是-2.分析 由条件利用正弦定理求得△ABC为等腰直角三角形,由△ABC的面积为$\frac{1}{2}$,求得三角形的各个边长,再利用两个向量的数量积的定义求得要求式子的值.
解答 解:在△ABC中,∵sinA:sinB:sinC=1:1:$\sqrt{2}$,利用正弦定理可得a:b:c=1:1:$\sqrt{2}$,
设a=b=k,则c=$\sqrt{2}$k,∴△ABC为等腰直角三角形,A=B=$\frac{π}{4}$,C=$\frac{π}{2}$.
且△ABC的面积为$\frac{1}{2}$ab=$\frac{1}{2}$•k•k=$\frac{1}{2}$,∴k=1,
则$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$=$\sqrt{2}$•1cos$\frac{3π}{4}$+0+1•$\sqrt{2}$•cos$\frac{3π}{4}$=-2,
故答案为:-2.
点评 本题主要考查正弦定理,两个向量的数量积的定义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.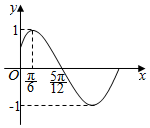 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则$\sum_{n=1}^{2016}$f($\frac{nπ}{6}$)=( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |
19.下列函数中与f(x)=2x+2-x具有相同的奇偶性的是( )
| A. | y=sinx | B. | y=x2+x+1 | C. | y=|x| | D. | y=|lgx| |
20.(理)某学习小组共12人,其中有五名是“三好学生”,现从该小组中任选5人参加竞赛,用ξ表示这5人中“三好学生”的人数,则下列概率中等于$\frac{C_7^5+C_5^1C_7^4}{{C_{12}^5}}$的是( )
| A. | P(ξ=1) | B. | P(ξ≤1) | C. | P(ξ≥1) | D. | P(ξ≤2) |