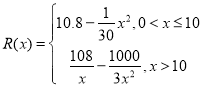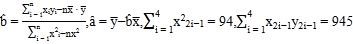题目内容
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)若函数![]() 在
在![]() 上恒有意义,求
上恒有意义,求![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]() ?若存在求出
?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据![]() 在
在![]() 上恒有意义,则
上恒有意义,则![]() 在
在![]() 上恒成立.讨论对称轴的位置,即可求得
上恒成立.讨论对称轴的位置,即可求得![]() 的取值范围.
的取值范围.
(2)讨论![]() 与
与![]() 两种情况,结合复函函数单调性即可判断是否符合单调递增.再根据最大值为
两种情况,结合复函函数单调性即可判断是否符合单调递增.再根据最大值为![]() ,代入
,代入![]() 的值,解方程即可求解.
的值,解方程即可求解.
(1)函数![]() 在
在![]() 上恒有意义
上恒有意义
即![]() 在
在![]() 上恒成立
上恒成立
令![]()
对称轴为![]() ,开口向上
,开口向上
当![]() 时,只需
时,只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
当![]() 时,只需
时,只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
当![]() 时, 只需
时, 只需![]() ,即
,即![]() ,解得
,解得![]() ,所以
,所以![]()
综上可知, ![]() 的取值范围为
的取值范围为![]()
(2)函数![]() 对称轴为
对称轴为![]()
由复合函数单调性的性质可知:
当![]() 时
时![]() 为单调递减函数,
为单调递减函数, ![]() 在
在![]() 上为单调递增函数,所以
上为单调递增函数,所以![]() 在
在![]() 上单调递减,不合题意
上单调递减,不合题意
当![]() 时,
时, ![]() 为单调递增函数, 若
为单调递增函数, 若![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上为单调递增函数.
上为单调递增函数.
所以由对称轴在![]() 左侧可得
左侧可得![]()
因为最大值为2,则![]()
即![]()
即![]() ,化简可得
,化简可得![]()
解得![]() 或
或 ![]()
因为![]()
所以![]()
当![]() 函数
函数![]() 在区间
在区间![]() 上为增函数,且最大值为
上为增函数,且最大值为![]()

【题目】为了解学生喜欢校内、校外开展活动的情况,某中学一课外活动小组在学校高一年级进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为
分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为![]() 类学生,低于60分的称为
类学生,低于60分的称为![]() 类学生.
类学生.

(1)根据已知条件完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为性别与是否为
的前提下认为性别与是否为![]() 类学生有关系?
类学生有关系?
|
| 合计 | |
男 | 110 | ||
女 | 50 | ||
合计 |
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中![]() 类学生的人数为
类学生的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某中学为调查该校学生每周参加社会实践活动的情况,随机收集了若干名学生每周参加社会实践活动的时间(单位:小时),将样本数据绘制如图所示的频率分布直方图,且在[0,2)内的学生有1人.
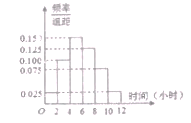
(1)求样本容量![]() ,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
,并根据频率分布直方图估计该校学生每周参加社会实践活动时间的平均值;
(2)将每周参加社会实践活动时间在[4,12]内定义为“经常参加社会实践”,参加活动时间在[0,4)内定义为“不经常参加社会实践”.已知样本中所有学生都参加了青少年科技创新大赛,有13人成绩等级为“优秀”,其余成绩为“一般”,其中成绩优秀的13人种“经常参加社会实践活动”的有12人.请将2×2列联表补充完整,并判断能否在犯错误的概率不超过0.05的前提下认为青少年科技创新大赛成绩“优秀”与经常参加社会实践活动有关;
(3)在(2)的条件下,如果从样本中“不经常参加社会实践”的学生中随机选取两人参加学校的科技创新班,求其中恰好一人成绩优秀的概率.
参考公式和数据:
![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |