题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,(
,(![]() )其图象上任意一点
)其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
【答案】
(3)因为方程![]() 有唯一实数解,
有唯一实数解,
所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,
,
则![]() .令
.令![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在(0,
在(0,![]() )上单调递减,
)上单调递减,
当![]() 时,
时,![]() ,
,![]() 在(
在(![]() ,+∞)单调递增
,+∞)单调递增
当![]() 时,
时,![]() =0,
=0,![]() 取最小值
取最小值![]() .(12′)
.(12′)

【解析】
(1)利用导数求函数的单调区间即得函数的最大值.(2)由题得![]() ,
,![]() .再求右边二次函数的最大值即得
.再求右边二次函数的最大值即得![]() .(3)转化为
.(3)转化为![]() 有唯一实数解,设
有唯一实数解,设![]() ,再研究函数在定义域内有唯一的零点得解.
,再研究函数在定义域内有唯一的零点得解.
(1)依题意,知![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() .(∵
.(∵![]() )
)
因为 ![]() 有唯一解,所以
有唯一解,所以![]() ,当
,当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
所以![]() 的极大值为
的极大值为![]() ,此即为最大值.
,此即为最大值.
(2)![]() ,
,![]() ,则有
,则有![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ,
,![]() .
.
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() .
.
(3)因为方程![]() 有唯一实数解,
有唯一实数解,
所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,
,
则![]() ,令
,令![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 取最小值
取最小值![]() .
.
则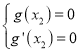 ,即
,即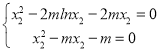 ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() (*)
(*)
设函数![]() ,因为当
,因为当![]() 时,
时,
![]() 是增函数,所以
是增函数,所以![]() 至多有一解,
至多有一解,
因为![]() ,所以方程(*)的解为
,所以方程(*)的解为![]() ,即
,即![]() ,解得
,解得![]() .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.

