题目内容
若点P（x，y）是曲线
+
=1上任意一点，则2x+
y的最小值为
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
-5
-5
．分析：利用参数法设出点的坐标，再利用辅助角公式化简，即可求得最小值．
解答：解：由题意，设P（2cosα，
sinα）（α∈R），则2x+
y=4cosα+3sinα=5sin（α+φ）
∴sin（α+φ）=-1时，2x+
y的最小值为-5
故答案为：-5
| 3 |
| 3 |
∴sin（α+φ）=-1时，2x+
| 3 |
故答案为：-5
点评：本题考查椭圆方程，考查参数法的运用，考查辅助角公式，正确设点是关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，成都市准备在南湖的一侧修建一条直路EF，另一侧修建一条观光大道，大道的前一部分为曲线段FBC，该曲线段是函数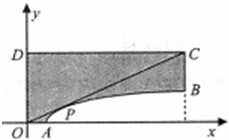
已知图形OAPBCD是由不等式组
为坐标原点，
,
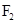是双曲线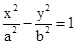
（a＞0，b＞0）的焦点，若在双曲
,则该双曲线的渐近线方程为(
)
y=0
B.
=0 D.
±y=0