题目内容
19.已知向量$\overrightarrow{a}$=(2,2,1),$\overrightarrow{b}$=(3,5,3),则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{3}$.分析 由已知条件利用空间向量坐标运算法则,先求出$2\overrightarrow{a}-\overrightarrow{b}$=(1,-1,-1),由此能求出|2$\overrightarrow{a}$-$\overrightarrow{b}$|.
解答 解:∵向量$\overrightarrow{a}$=(2,2,1),$\overrightarrow{b}$=(3,5,3),
∴$2\overrightarrow{a}-\overrightarrow{b}$=(4,4,2)-(3,5,3)=(1,-1,-1),
|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{1+1+1}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查向量的模的求法,是基础题,解题时要认真审题,注意向量的坐标运算法则的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在△ABC中,内角A、B、C的对边分别是a、b、c,若a+b≥2c,则∠C的最大度数是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
4.设m.n是两条不同的直线,α是一个平面,下列命题中正确的是( )
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,m⊥n,则n∥α | D. | m⊥α,m∥n,则n⊥α |
11.“a,b是异面直线”是指( )
| A. | a?平面a,b?平面β且α∩β=∅ | B. | a?平面α,b?平面α | ||
| C. | a?平面α,b?平面β | D. | a∩b=∅且a不平行于b |
9.把圆周8等分,得8个等分点,以这些点为顶点作三角形可得56个三角形,从这些三角形中任取一个三角形是锐角三角形的概率P=( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
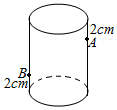 圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)
圆柱形玻璃杯高8cm,杯口周长为12cm,内壁距杯口2cm的点A处有一点蜜糖.A点正对面的外壁(不是A点的外壁)距杯底2cm的点B处有一小虫.若小虫沿杯壁爬向蜜糖饱食一顿,最少要爬多少10cm.(不计杯壁厚度与小虫的尺寸)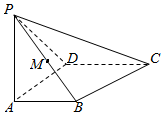 四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.
四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点,求直线CM与平面ABCD所成角的正弦值.