题目内容
20.若不等式组$\left\{\begin{array}{l}{x+y≤1}\\{x-y≥-1}\\{y≥0}\end{array}\right.$所表示的平面区域被直线z=x-y分成面积相等的两部分,则z的值为( )| A. | $-\frac{1}{2}$ | B. | $-\frac{\sqrt{2}}{2}$ | C. | 1-2$\sqrt{2}$ | D. | 1$-\sqrt{2}$ |
分析 作出不等式组对应的平面区域,根据平面区域面积的关系进行求解即可.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则A(-1,0),B(1,0),C(0,1),则三角形ABC的面积S=$\frac{1}{2}×2×1$=1,
若不等式组所表示的平面区域被直线z=x-y分成面积相等的两部分,
则三角形BDE的面积S=$\frac{1}{2}$,
当y=0时,x=z,则-1≤z≤1,即D(z,0),
由$\left\{\begin{array}{l}{x-y=z}\\{x+y=1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1+z}{2}}\\{y=\frac{1-z}{2}}\end{array}\right.$,即E的纵坐标为y=$\frac{1-z}{2}$,
则三角形BDE的面积S=$\frac{1}{2}$=$\frac{1}{2}$(1-z)•$\frac{1-z}{2}$,
得(1-z)2=2,则1-z=±$\sqrt{2}$,
即z=1±$\sqrt{2}$,
∵-1≤z≤1,∴z=1-$\sqrt{2}$,
故选:D.
点评 本题主要考查线性规划的应用,结合三角形的面积公式是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
15.已知函数$f(x)=sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$,其图象相邻两条对称轴之间的距离为$\frac{π}{2}$,且函数$f(x+\frac{π}{12})$是偶函数,则下列判断正确的是( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)在区间$[\frac{3π}{4},π]$上单调递增 | |
| C. | 函数f(x)的图象关于直线$x=-\frac{7π}{12}$对称 | |
| D. | 函数f(x)的图象关于点$(\frac{7π}{12},0)$对称 |
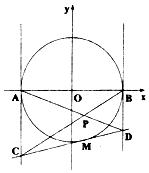 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.