题目内容
已知等比数列![]() 的各项均为正数,且
的各项均为正数,且![]() .
.
(I)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 求使
求使![]() 恒成立,求实数k范围。
恒成立,求实数k范围。
解:(Ⅰ)设数列{an}的公比为q,由![]() 得
得![]() 所以
所以![]() .
.
由条件可知q>0,故![]() . (3分)
. (3分)
由![]() 得
得![]() ,所以
,所以![]() .(6分)
.(6分)
故数列{an}的通项式为an=![]() . (7分)
. (7分)
(Ⅱ )![]()
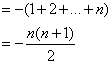 (9分)
(9分)
故![]() (10分)
(10分)
![]() (11分)
(11分)
所以数列![]() 的前n项和为
的前n项和为![]() 。化简得
。化简得![]() 对任意
对任意![]() 恒成立
恒成立
设![]() ,则
,则![]()
当![]() ,
,![]() ,
,![]() 为单调递减数列,当
为单调递减数列,当![]() ,
,![]() ,
,![]() 为单调递增数列
为单调递增数列
![]() ,所以,
,所以, ![]() 时,
时, ![]() 取得最大值
取得最大值![]()
所以, 要使![]() 对任意
对任意![]() 恒成立,
恒成立,![]() …………14分
…………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的各项均为正数,公比
的各项均为正数,公比 ,设
,设 ,
, ,则
,则 与
与 的大小关系是
的大小关系是  B.
B. C.
C. D.无法确定
D.无法确定 ,定义数列
,定义数列 为数列
为数列 =2,
=2,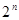 ,则数列
,则数列 =
=  ,
, ,则
,则 =
=
 的各项均为正数,且
的各项均为正数,且 .
. ,求数列
,求数列 的前n项和.
的前n项和. ,求数列{
,求数列{ }的前
}的前 项和.
项和. 的各项均为正数,且
的各项均为正数,且
 ,求数列
,求数列 的前n项和
的前n项和