题目内容
(本题满分12分)已知函数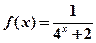
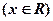 。
。
(Ⅰ)试证函数f(x)的图象关于点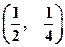 对称;
对称;
(Ⅱ)若数列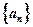 的通项公式为
的通项公式为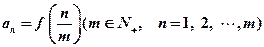 , 求数列
, 求数列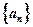 的前
的前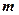 项和
项和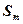 ;
;
(Ⅲ)设数列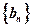 满足:
满足: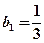 ,
,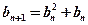 。设
。设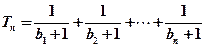 。若(Ⅱ)中的
。若(Ⅱ)中的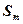 满足对任意不小于2的正整数
满足对任意不小于2的正整数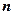 ,
,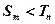 恒成立,试求
恒成立,试求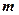 的最大值。
的最大值。
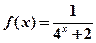
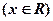 。
。(Ⅰ)试证函数f(x)的图象关于点
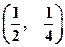 对称;
对称;(Ⅱ)若数列
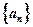 的通项公式为
的通项公式为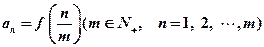 , 求数列
, 求数列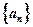 的前
的前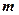 项和
项和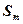 ;
;(Ⅲ)设数列
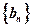 满足:
满足: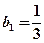 ,
,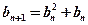 。设
。设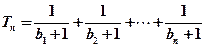 。若(Ⅱ)中的
。若(Ⅱ)中的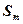 满足对任意不小于2的正整数
满足对任意不小于2的正整数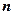 ,
,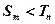 恒成立,试求
恒成立,试求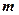 的最大值。
的最大值。(Ⅰ)证明略。
(Ⅱ)
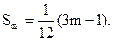
(Ⅲ)6
解:
(Ⅰ)设点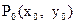 是函数
是函数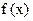 的图象上任意一点, 其关于点
的图象上任意一点, 其关于点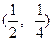 的对称点为
的对称点为 由
由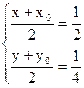 得
得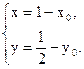
所以, 点P的坐标为P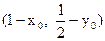
由点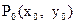 在函数
在函数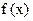 的图象上, 得
的图象上, 得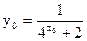
∵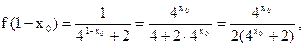

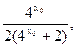 ∴点P
∴点P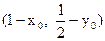 在函数
在函数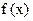 的图象上
的图象上
∴函数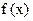 的图象关于点
的图象关于点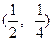 对称
对称
(Ⅱ)由(Ⅰ)可知,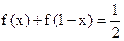 , 所以
, 所以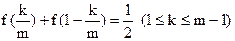 ,
,
即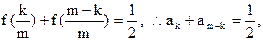
由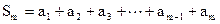 , ………………①
, ………………①
得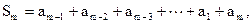 ………………②
………………②
由①+②, 得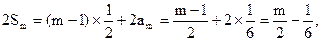
∴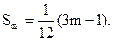
(Ⅲ)∵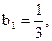
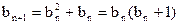 , ………………③
, ………………③
∴对任意的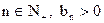 . ………………④
. ………………④
由③、④, 得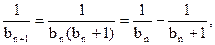 即
即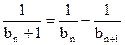
∴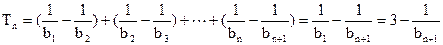
∵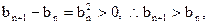 ∴数列
∴数列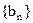 是单调递增数列
是单调递增数列
∴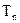 关于n递增. 当
关于n递增. 当 , 且
, 且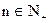 时,
时, 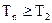
∵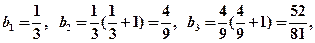
∴
∴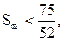 即
即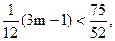 ∴
∴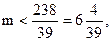 ∴m的最大值为6。
∴m的最大值为6。
(Ⅰ)设点
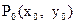 是函数
是函数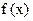 的图象上任意一点, 其关于点
的图象上任意一点, 其关于点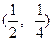 的对称点为
的对称点为 由
由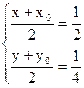 得
得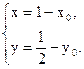
所以, 点P的坐标为P
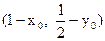
由点
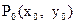 在函数
在函数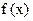 的图象上, 得
的图象上, 得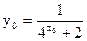
∵
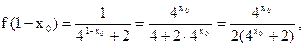

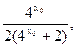 ∴点P
∴点P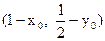 在函数
在函数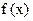 的图象上
的图象上∴函数
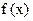 的图象关于点
的图象关于点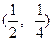 对称
对称(Ⅱ)由(Ⅰ)可知,
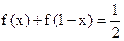 , 所以
, 所以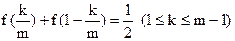 ,
,即
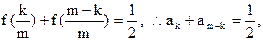
由
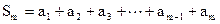 , ………………①
, ………………①得
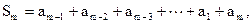 ………………②
………………②由①+②, 得
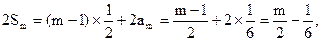
∴
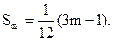
(Ⅲ)∵
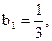
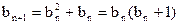 , ………………③
, ………………③∴对任意的
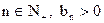 . ………………④
. ………………④由③、④, 得
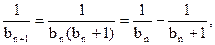 即
即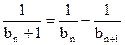
∴
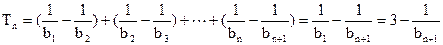
∵
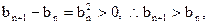 ∴数列
∴数列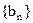 是单调递增数列
是单调递增数列∴
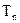 关于n递增. 当
关于n递增. 当 , 且
, 且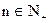 时,
时, 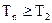
∵
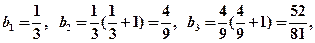
∴

∴
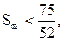 即
即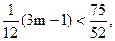 ∴
∴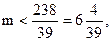 ∴m的最大值为6。
∴m的最大值为6。
练习册系列答案
相关题目
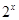 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=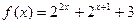 ,求
,求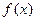 的值域。
的值域。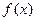 满足:x≥4,则
满足:x≥4,则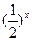 ;当x<4时
;当x<4时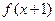 ,则
,则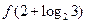 =( )
=( )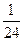 B
B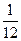 C
C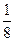 D
D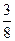
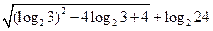 ="______________."
="______________." 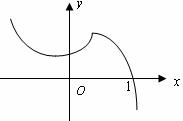
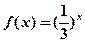 ,若
,若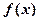 的图象关于直线
的图象关于直线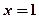 对称的图象对应的函数为
对称的图象对应的函数为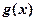 ,则
,则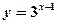



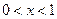 ,则
,则 ,
, ,
, 之间的大小关系为 ( )
之间的大小关系为 ( ) 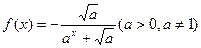 的图像关于点
的图像关于点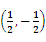 对称,
对称,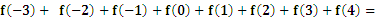 _________________.
_________________. 的定义域为
的定义域为 ,若对于任意
,若对于任意 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③ ,则
,则 等于 ( )
等于 ( ) 


