题目内容
已知抛物线y=x2+1与双曲线
-
=1(a>0,b>0)的渐近线没有公共点,则此双曲线的离心率可以
是( )
(A)
(B) 
(C)
(D)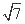
A
解析:双曲线的渐近线为y=±
x,
由
消去y整理得x2-x+1=0.
∵双曲线的渐近线与抛物线没有交点,
∴Δ=（-）2-4<0,
即<2.
∴双曲线的离心率e=
=
∈(1, ),
所以只有选项A满足条件.故选A.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案
=3,则C的方程为( )
+y2=1 (B)
+
=1
+ 
=1 (D)
+
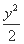=1
b）,又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B（0,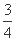
b）,且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
,0),(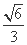 
.直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
D.