题目内容
12．若直线y=kx+1与双曲线x2-y2=2的左支交于不同的两点，则k的取值范围是（1，$\frac{\sqrt{6}}{2}$）．分析 根据直线y=kx+1与双曲线x2-y2=1的左支交于不同的两点，可得直线与双曲线联立方程有两个不等的负根，进而构造关于k的不等式组，解不等式可得答案．
解答 解：联立方程直线y=kx+1与双曲线x2-y2=2得
（1-k2）x2-2kx-3=0…①
若直线y=kx+1与双曲线x2-y2=2的左支交于不同的两点，
则方程①有两个不等的负根，
∴$\left\{\begin{array}{l}{4{k}^{2}+12（1-{k}^{2}）＞0}\\{\frac{2k}{1-{k}^{2}}＜0}\\{\frac{-3}{1-{k}^{2}}＞0}\end{array}\right.$，
解得：k∈（1，$\frac{\sqrt{6}}{2}$）
故答案为：（1，$\frac{\sqrt{6}}{2}$）．
点评 本题考查的知识点圆锥曲线中的范围问题，其中分析出题目的含义是直线与双曲线联立方程有两个不等的负根，是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
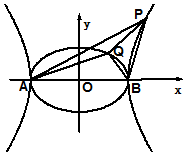已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点，P、Q分别为双曲线和椭圆上不同于两点A、B的动点，且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ（$\overrightarrow{OA}$+$\overrightarrow{QB}$）（λ∈R，|λ|＞1），设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4的值（ ）
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点，P、Q分别为双曲线和椭圆上不同于两点A、B的动点，且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ（$\overrightarrow{OA}$+$\overrightarrow{QB}$）（λ∈R，|λ|＞1），设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4的值（ ）| A． | 大于0 | B． | 等于0 | ||
| C． | 小于0 | D． | 大于0，等于0，小于0都有可能 |
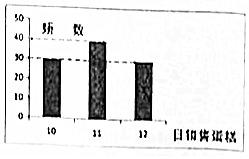某超市每两天购入一批某型号的生日蛋糕进行销售，进价50元/个，售价60元/个，若每次购入的生日蛋糕两天内没有售完，则以40元/个的价格可以全部处理掉，根据此超市以往随机抽取的100天此类蛋糕的销售情况，如柱形图所示．设n为每次购入的蛋糕数，ξ为两天内的蛋糕销售数量，W为此批购入的蛋糕销售的利润（视频率为概率，且每天销售情况是独立的）
1．设数列{an}的通项公式为an=3n，且a2，a4，ak成等比数列，则数列k的值为（ ）
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
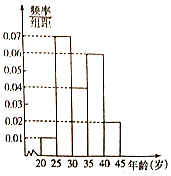今年我国许多省市雾霾频发，为增强市民的环境保护意识，某市面向全市学校征召100名教师做义务宣传志愿者，成立环境保护宣传组，现把该组的成员按年龄分成5组：第一组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45），得到的频率分布直方图如图所示．