题目内容
已知ABCD—A1B1C1D1是正方体.(1)求A1C1与B1C所成角的大小;
(2)求A1C与AD1所成角的大小;
(3)若E、F分别为AB、AD的中点,求A1C1与EF以及AD1与EF所成角的大小.
解析:(1)如下图甲中,连结AC、AB1.由A1C是正方体,知AA1![]() CC1,故A1ACC1是平行四边形,所以AC∥A1C1.从而B1C与AC所成的角就是A1C1与B1C所成的角.
CC1,故A1ACC1是平行四边形,所以AC∥A1C1.从而B1C与AC所成的角就是A1C1与B1C所成的角.
由AB1=AC=B1C,知∠B1CA=60°,即A1C1与B1C所成的角为60°
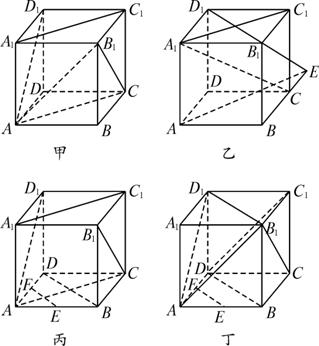
(2)如图乙中,延长BC到E,使CE=BC,连结D1E、AE,由BC![]() A1D1,知CE
A1D1,知CE![]() A1D1,故四边形A1CED1是平行四边形,所以D1E∥A1C.从而D1E与AD1所成的角就是A1C与AD1所成的角.
A1D1,故四边形A1CED1是平行四边形,所以D1E∥A1C.从而D1E与AD1所成的角就是A1C与AD1所成的角.
设正方体的棱长为a,则
AD1=![]() ,A1C=
,A1C=![]() ,
,![]() .
.
由余弦定理,知
cos∠AD1E=![]() .
.
所以A1C与AD1所成的角为90°.
(3)如图丙中,连结AC、BD,由A1A![]() CC1,知A1ACC1是平行四边形,故AC∥A1C1,所以AC与EF所成的角就是A1C1与EF所成的角.由EF是△ABD的中位线,知EF∥BD,知EF⊥AC,即所求角为90°.在图丁中,连结BD、D1B1.由DD1
CC1,知A1ACC1是平行四边形,故AC∥A1C1,所以AC与EF所成的角就是A1C1与EF所成的角.由EF是△ABD的中位线,知EF∥BD,知EF⊥AC,即所求角为90°.在图丁中,连结BD、D1B1.由DD1![]() BB1,知B1BDD1是平行四边形,故D1B1∥DB,又由EF是△ABD的中位线,知EF∥BD,故EF∥B1D1,所以AD1与B1D1所成的角就是AD1与EF所成的角.连结AB1,由AB1=AD1=D1B1,知AD1与D1B所成角为60°,即有AD1与EF所成角为60°.
BB1,知B1BDD1是平行四边形,故D1B1∥DB,又由EF是△ABD的中位线,知EF∥BD,故EF∥B1D1,所以AD1与B1D1所成的角就是AD1与EF所成的角.连结AB1,由AB1=AD1=D1B1,知AD1与D1B所成角为60°,即有AD1与EF所成角为60°.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 已知正方体ABCD-A1B1C1D1的棱长为a,
已知正方体ABCD-A1B1C1D1的棱长为a, 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点.
如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.