题目内容
已知向量
=（cosx，y），
=（
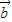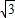sinx+cosx，-1）（x，y∈R）且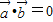
（1）求y与x的函数关系y=f（x）的表达式；
（2）当x∈[0，
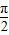]时，求满足f（x）=1的x值．
【答案】分析：（1）由 
=0，以及两角和差的三角公式可得 y=sin（2x+
）+
，从而求得f（x）的解析式．
（2）由f（x）=1，可得sin（2x+
）=
．再由x∈[0，
π]求得x的值．
解答：解：（1）由
=
sinxcosx+cos2x-y=0，可得
y=
sinx?cosx+cos2x=
sin2x+
cos2x+
=sin（2x+
）+
∴f（x）=sin（2x+
）+
．
（2）∵f（x）=1，∴sin（2x+
）=
．
又∵x∈[0，
π]，∴
≤2x+
≤
，
∴2x+
=
或2x+
=
，
∴x=0或
．
点评：本题主要考查两个向量的数量积的定义，两角和差的三角公式的应用，正弦函数的定义域和值域，属于中档题．
=0，以及两角和差的三角公式可得 y=sin（2x+）+，从而求得f（x）的解析式．（2）由f（x）=1，可得sin（2x+
）=．再由x∈[0，π]求得x的值．解答：解：（1）由
=sinxcosx+cos2x-y=0，可得y=
sinx?cosx+cos2x=sin2x+cos2x+=sin（2x+）+∴f（x）=sin（2x+
）+．（2）∵f（x）=1，∴sin（2x+
）=．又∵x∈[0，
π]，∴≤2x+≤，∴2x+
=或2x+=，∴x=0或
．点评：本题主要考查两个向量的数量积的定义，两角和差的三角公式的应用，正弦函数的定义域和值域，属于中档题．
练习册系列答案
相关题目