题目内容
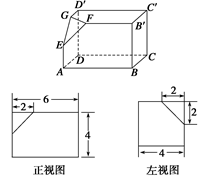
如图,在棱长为1的正方体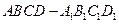 中,
中,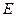 、
、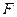 、
、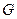 分别是棱
分别是棱 、
、 、
、 的中点.
的中点.
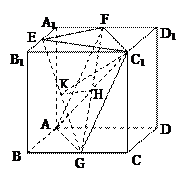
(Ⅰ)求证: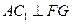 ;
;
(Ⅱ)求点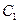 到平面
到平面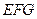 的距离;
的距离;
(Ⅲ)求二面角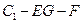 的大小.
的大小.
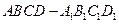 中,
中,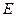 、
、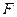 、
、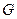 分别是棱
分别是棱 、
、 、
、 的中点.
的中点.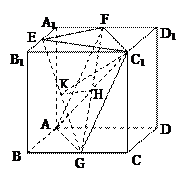
(Ⅰ)求证:
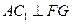 ;
;(Ⅱ)求点
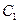 到平面
到平面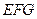 的距离;
的距离;(Ⅲ)求二面角
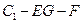 的大小.
的大小.(Ⅰ)证明略;
(Ⅱ)点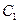 到平面
到平面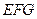 的距离为
的距离为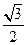 ;
;
(Ⅲ)二面角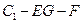 的大小是
的大小是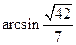 .
.
(Ⅱ)点
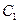 到平面
到平面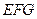 的距离为
的距离为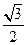 ;
;(Ⅲ)二面角
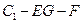 的大小是
的大小是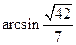 .
.(Ⅰ)证明:连结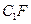 、
、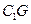 、
、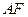 、
、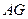 ,
,
∵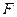 、
、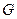 分别是棱
分别是棱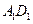 、
、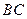 的中点,由全等的正方形中对应的线段长度相等可得
的中点,由全等的正方形中对应的线段长度相等可得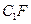 =
=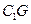 =
=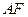 =
=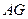 ,∴四边形
,∴四边形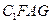 是菱形,∴
是菱形,∴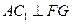 .
.
(Ⅱ)解: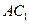 在面
在面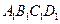 上的射影是
上的射影是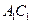 ,
, ,∴
,∴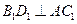 .
.
∵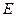 、
、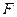 分别是棱
分别是棱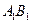 、
、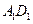 的中点,∴
的中点,∴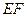 ∥
∥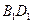 ,∴
,∴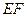
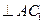 .
.
由(Ⅰ)有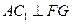 ,
,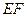 与
与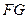 是平面
是平面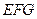 内两相交直线,∴
内两相交直线,∴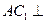 平面
平面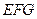 .
.
设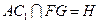 ,则
,则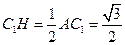 ,即点
,即点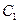 到平面
到平面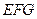 的距离等于
的距离等于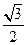 .
.
(Ⅲ)解:取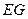 的中点
的中点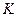 ,连结
,连结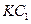 、
、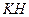 ,由全等的正方形中对应的线段长度相等可得
,由全等的正方形中对应的线段长度相等可得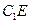 =
=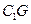 ,∴
,∴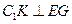 ,由(Ⅱ)有
,由(Ⅱ)有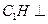 平面
平面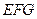 ,∴
,∴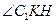 是二面角
是二面角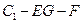 的平面角.
的平面角.
在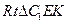 中,
中,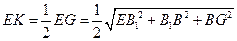
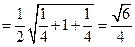 ,
,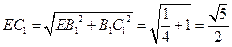 ,
,
∴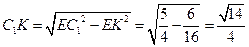 .
.
在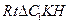 中,
中,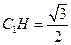 ,
,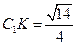 ,∴
,∴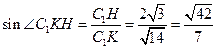 .
.
∴ 二面角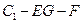 的大小是
的大小是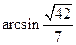 .
.
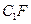 、
、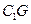 、
、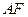 、
、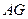 ,
,∵
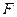 、
、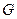 分别是棱
分别是棱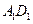 、
、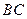 的中点,由全等的正方形中对应的线段长度相等可得
的中点,由全等的正方形中对应的线段长度相等可得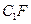 =
=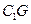 =
=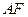 =
=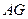 ,∴四边形
,∴四边形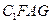 是菱形,∴
是菱形,∴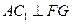 .
. (Ⅱ)解:
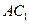 在面
在面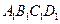 上的射影是
上的射影是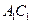 ,
, ,∴
,∴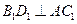 .
.∵
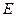 、
、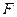 分别是棱
分别是棱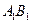 、
、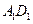 的中点,∴
的中点,∴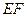 ∥
∥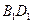 ,∴
,∴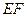
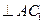 .
. 由(Ⅰ)有
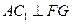 ,
,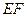 与
与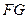 是平面
是平面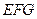 内两相交直线,∴
内两相交直线,∴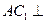 平面
平面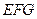 .
.设
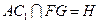 ,则
,则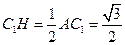 ,即点
,即点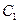 到平面
到平面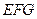 的距离等于
的距离等于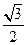 .
.(Ⅲ)解:取
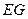 的中点
的中点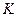 ,连结
,连结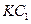 、
、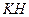 ,由全等的正方形中对应的线段长度相等可得
,由全等的正方形中对应的线段长度相等可得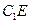 =
=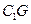 ,∴
,∴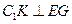 ,由(Ⅱ)有
,由(Ⅱ)有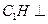 平面
平面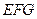 ,∴
,∴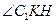 是二面角
是二面角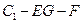 的平面角.
的平面角. 在
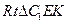 中,
中,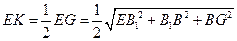
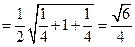 ,
,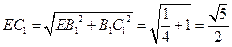 ,
,∴
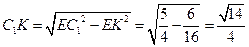 .
. 在
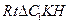 中,
中,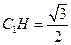 ,
,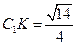 ,∴
,∴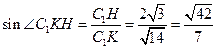 .
.∴ 二面角
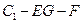 的大小是
的大小是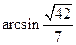 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
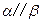 ,
,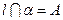 ,求证
,求证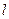 与
与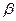 相交.
相交.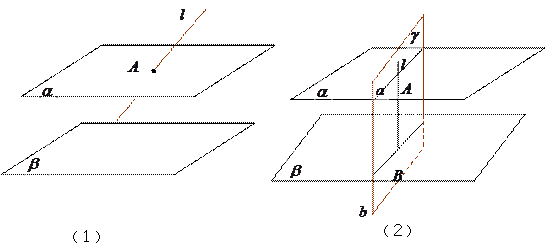
 中
中 ,
,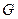 分别为
分别为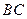 ,
,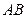 的中点,
的中点,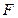 在
在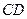 上,
上,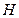 在
在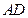 上,且有
上,且有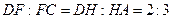 ,求证:
,求证: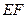 ,
,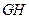 ,
,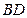 交于一点.
交于一点.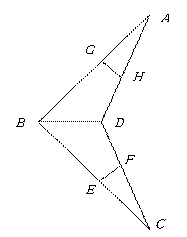

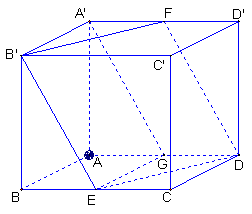
 a,M是AD的中点。
a,M是AD的中点。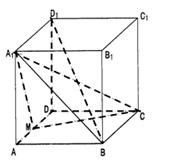
 平面
平面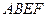 ,
,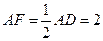 ,
,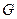 是
是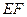 的中点。
的中点。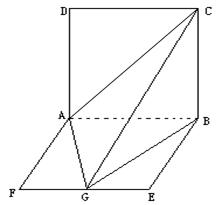
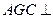 平面
平面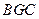 ;(2)求四面体
;(2)求四面体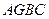 的体积。
的体积。  的8个顶点都在球O的表面上,则球O的表面积是 设
的8个顶点都在球O的表面上,则球O的表面积是 设 分别是该正方形的棱
分别是该正方形的棱 的中点,则直线
的中点,则直线 被球O截得的线段长为 .
被球O截得的线段长为 .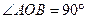 ,
,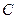 为空间中一点,且
为空间中一点,且 ,则直线
,则直线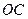 与平面
与平面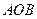 所成角
所成角 的正弦值为
的正弦值为