题目内容
9.欧拉(Leonhard Euler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占用非常重要的地位,被誉为“数学中的天桥”,根据此公式可知,e-4i表示的复数在复平面中位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 e-4i=cos(-4)+isin(-4),再利用诱导公式与三角函数求值即可得出.
解答 解:e-4i=cos(-4)+isin(-4),∵cos(-4)=cos[π+(4-π)]=-cos(4-π)<0,sin(-4)=-sin[π+(4-π)]=sin(4-π)>0,
∴e-4i表示的复数在复平面中位于第二象限.
故选:B.
点评 本题考查了欧拉公式、诱导公式与三角函数求值,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.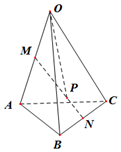 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
 已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
已知M、N分别是四面体OABC的棱OA,BC的中点,点P在线MN上,且MP=2PN,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
17.函数y=f(x)满足对任意x∈R都有f(x+2)=f(-x)成立,且函数y=f(x-1)的图象关于点(1,0)对称,f(1)=4,则f(2016)+f(2017)+f(2018)=( )
| A. | 12 | B. | 8 | C. | 4 | D. | 0 |
4.已知函数f(x)=sin(2x+$\frac{π}{6}$)+cos2x,则f(x)的一个单调递减区间是( )
| A. | [$\frac{π}{12}$,$\frac{7π}{12}$] | B. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | C. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | D. | [-$\frac{π}{6}$,$\frac{5π}{6}$] |
14.已知集合A={x|x2-6x+5≤0},B={x|y=log2(x-2)},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |