题目内容
6.设当x=θ时,函数f(x)=sinx-2cos2 $\frac{x}{2}$取得最大值$\sqrt{2}-1$.分析 根据二倍角的余弦公式和两角差的正弦公式即可得出$f(x)=\sqrt{2}sin(x-\frac{π}{4})-1$,从而便可得出f(x)的最大值.
解答 解:$f(x)=sinx-cosx-1=\sqrt{2}sin(x-\frac{π}{4})-1$;
∴$sin(x-\frac{π}{4})=1$时,f(x)取得最大值$\sqrt{2}-1$.
故答案为:$\sqrt{2}-1$.
点评 考查二倍角的余弦公式,以及两角差的正弦公式,正弦函数的最大值.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
16.已知A={锐角},B={第一象限角},C={小于90°的角},那么A,B,C的关系式( )
| A. | A=B∩C | B. | B⊆C | C. | A∪C=C | D. | A=B=C |
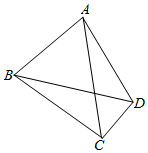 如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.
如图,在四边形ABCD中,AB=BD=$\sqrt{2}$,AC=$\sqrt{6}$,AD=2,∠ABC=120°.