题目内容
△ 的三个内角
的三个内角 的对边的长分别为
的对边的长分别为 ,有下列两个条件:①
,有下列两个条件:① 成等差数列;②
成等差数列;② 成等比数列,现给出三个结论:(1)
成等比数列,现给出三个结论:(1) ;(2)
;(2) ;(3)
;(3) 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①__________________________________________
②__________________________________________
(II)证明:
解:(Ⅰ)命题一:△ABC中,若a、b、c成等差数列,求证:(1) ;(2)
;(2) ;
;
命题二:△ABC中,若a、b、c成等差数列,求证:(1) ; (2)
; (2) ;
;
命题三:△ABC中,若a、b、c成等差数列,求证:(1) ; (2)
; (2) ;
;
命题四:△ABC中,若a、b、c成等比数列,求证:(1) ; (2)
; (2) ;
;
(答案不唯一)
(Ⅱ)下面给出命题一、二、三的证明:
(1)∵a、b、c成等差数列,∴2b=a+c,∴ ,
,
∴ ,
,
且B∈(0, ),∴
),∴ ;
;
(2)

 ;
;
(3) ,
,
∵ ,∴
,∴ ,∴
,∴ ,
,
∴ 。
。
下面给出命题四的证明:
(4)∵a、b、c成等比数列,∴b2=a+c,
∴ ,
,
且 ,∴
,∴ 。
。

练习册系列答案
相关题目
 个小球,且每个小球的球面上要么只写有数字“
个小球,且每个小球的球面上要么只写有数字“ ”,要么只写有文字“奥运会” .假定每个小球每一次被取出的机会都相同,又知从中摸出
”,要么只写有文字“奥运会” .假定每个小球每一次被取出的机会都相同,又知从中摸出 个球都写着“奥运会”的概率是
个球都写着“奥运会”的概率是 .现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有一人取得写着文字“奥运会”的球时游戏终止.
.现甲、乙两个小朋友做游戏,方法是:不放回从口袋中轮流摸取一个球,甲先取、乙后取,然后甲再取,直到两个小朋友中有一人取得写着文字“奥运会”的球时游戏终止. 的概率分布列和期望E
的概率分布列和期望E .
. ,则
,则 的值______________.
的值______________. 中,
中, 为其前
为其前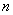 项和,若
项和,若 ,
, ,则
,则 为( )
为( ) 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 )的最大值为8,则
)的最大值为8,则 的最小值为________.
的最小值为________. 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则 ( )
( ) C.3 D.
C.3 D. 
 ,
, 则
则 _____________.
_____________.  }中,若点
}中,若点 在经过点(5,3)的定直线l上,求数列{
在经过点(5,3)的定直线l上,求数列{ 的值.
的值.  的值域为
的值域为