题目内容
已知,|
|=|
|=2,
与
的夹角为
,则
+
在
上的投影为 .
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| a |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:根据两个向量的模长和夹角做出两个向量的和
的模长,看出两个向量的和与的夹角,有向量的夹角和模长用向量的投影公式得到结果.
| a |
解答:
解:∵|
|=|
|=2,
与
的夹角为
,
∴|
+
|2=4+4+2|
||
|cos
=12,
∴|
+
|=2
,
∵
+
与
的夹角为
,
∴
+
在
上的投影为|
+
|cos
=3

故答案为:3
| a |
| b |
| a |
| b |
| π |
| 3 |
∴|
| a |
| b |
| a |
| b |
| π |
| 3 |
∴|
| a |
| b |
| 3 |
∵
| a |
| b |
| a |
| π |
| 6 |
∴
| a |
| b |
| a |
| a |
| b |
| π |
| 6 |

故答案为:3
点评:本题考查向量的投影,在计算投影的时注意看清楚是哪一个向量在哪一个向量上的投影,再用模长乘以夹角的余弦.

练习册系列答案
相关题目
曲线y=
+1(-2≤x≤2)与直线y=kx-2k+4有两个不同的交点时实数k的范围是( )
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-∞,
|
下列叙述中,正确的是( )
| A、四边形是平面图形 |
| B、有三个公共点的两个平面重合 |
| C、两两相交的三条直线必在同一个平面内 |
| D、三角形必是平面图形 |
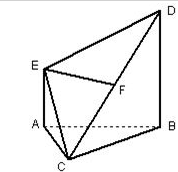 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.