Question

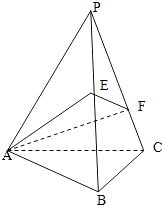
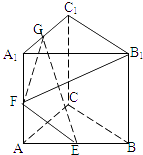
【题目】如图为一简单组合体，其底面ABCD为正方形，棱PD与EC均垂直于底面ABCD，PD=2EC，N为PB的中点，求证：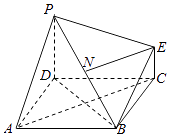

（1）平面EBC∥平面PDA；
（2）NE⊥平面PDB．

Answer 1

【答案】
（1）证明：∵PD⊥平面ABCD，CE⊥平面ABCD，∴EC∥PD，

又PD平面PDA，EC平面PDA，

∴EC∥平面PDA，

∵四边形ABCD为正方形，

∴BC∥AD，又AD平面PDA，BC平面PDA，

∴BC∥平面PDA，

∵EC平面EBC，BC平面EBC，EC∩BC=C，

∴平面EBC∥平面PDA

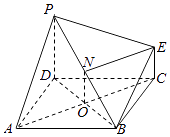
（2）证明：设AC与BD相交于点O，连接NO，

∵四边形ABCD为正方形，∴O为BD的中点，又N为PB的中点，

∴NO∥PD且NO= PD，

又由（1）得EC∥PD，且 ，

∴NO∥EC且NO=EC，∴四边形NOCE为平行四边形，

∴NE∥OC，即NE∥A，C

∵PD⊥平面ABCD，AC平面ABCD，∴AC⊥PD，

又DB⊥AC，PD∩BD=D

∴AC⊥平面PBD，又NE∥AC，

∴NE⊥平面PDB．

【解析】（1）由线面垂直性质得EC∥PD，由四边形ABCD为正方形，得BC∥AD，由此能证明平面EBC∥平面PDA．（2）推导出四边形NOCE为平行四边形，从而AC⊥PD，再由DB⊥AC，能证明NE⊥平面PDB．
【考点精析】本题主要考查了平面与平面平行的判定和直线与平面垂直的判定的相关知识点，需要掌握判断两平面平行的方法有三种:用定义；判定定理；垂直于同一条直线的两个平面平行；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．