题目内容
设人的某一特征（如眼睛大小）是由他的一对基因所决定的，以d表示显性基因，r表示隐性基因，则具有dd基因的人为纯显性，具有rr基因的人是纯隐性，具有rd基因的人为混合性．纯显性与混合性的人都露显性基因决定的某一特征，孩子从父母身上各得到1个基因，假定父母都是混合性．
问：（1）1个孩子有显性基因决定的特征的概率是多少？
（2）2个孩子中至少有一个有显性基因决定的特征的概率是多少？
解：因为父母都是混合性．即rd型的，
易得到孩子的一对基因为dd，rr，rd的概率分别为
，，
，
（1）孩子有显性决定的特征是具有dd，rd，所以：1个孩子有显性决定的特征的概率为+=
．
（2）因为2个孩子如果都不具有显性决定的特征．即2个孩子都具有rr基因的纯隐性特征，其概率为•=
．所以2个孩子中至少有一个显性决定特征的概率为1-=
．
分析：对于（1）求1个孩子有显性基因决定的特征的概率是多少，因为有显性基因决定的特征有2中可能纯显性dd，和混合体rd，分别求出2种可能性的概率相加即可得到答案．
对于（2）求2个孩子中至少有一个有显性基因决定的特征的概率，对于至少问题可以考虑求其反面没有显性基因决定的特征，即2个孩子都具有rr基因的纯隐性特征，然后用1减去它即可得到答案．
点评：此题主要考查相互独立事件的概率乘法公式在求基因问题中的应用，题中涉及到“至少”问题的求解，利用求反面的思想．这类题目属于数学与生物的结合，同学们需要注意．
易得到孩子的一对基因为dd，rr，rd的概率分别为
，，，（1）孩子有显性决定的特征是具有dd，rd，所以：1个孩子有显性决定的特征的概率为
+=．（2）因为2个孩子如果都不具有显性决定的特征．即2个孩子都具有rr基因的纯隐性特征，其概率为
•=．所以2个孩子中至少有一个显性决定特征的概率为1-=．分析：对于（1）求1个孩子有显性基因决定的特征的概率是多少，因为有显性基因决定的特征有2中可能纯显性dd，和混合体rd，分别求出2种可能性的概率相加即可得到答案．
对于（2）求2个孩子中至少有一个有显性基因决定的特征的概率，对于至少问题可以考虑求其反面没有显性基因决定的特征，即2个孩子都具有rr基因的纯隐性特征，然后用1减去它即可得到答案．
点评：此题主要考查相互独立事件的概率乘法公式在求基因问题中的应用，题中涉及到“至少”问题的求解，利用求反面的思想．这类题目属于数学与生物的结合，同学们需要注意．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知向量
=（2cosx，1），
=（cosx，
sin2x），f（x）=
（1）求f（x）的最小正周期和最大值；
（2）在△ABC中，a，b，c分别是角A、B、C的对边，且f（A）=2，a=，b=1，求角C．
为了调查胃病是否与生活规律有关，对某地70名40岁以上的人进行调查，结果如下：
| 患胃病 | 未患胃病 | 合计 | |
| 生活无规律 | 5 | 15 | 20 |
| 生活有规律 | 40 | 10 | 50 |
| 合计 | 45 | 25 | 70 |
参考数据：
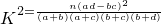
| P（K2≥k0） | 0.5 | 0.10 | 0.010 | 0.001 |
| k0 | 0.455 | 2.706 | 6.635 | 10.828 |
- A.99.9%
- B.99%
- C.没有充分的证据显示有关
- D.1%
；
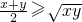=（2sinc，-
=（cos2c，
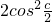-1）且