题目内容
曲线C上的动点P到定点Q（1，0）与它到直线x+1=0的距离相等．求：
（1）曲线C的方程；
（2）过点Q的直线l与曲线C交于A、B两点，求证：
•
为定值．
（温馨提示：
={x1，y1}
={x2，y2}，则
•
=x1x2+y1y2）
（1）曲线C的方程；
（2）过点Q的直线l与曲线C交于A、B两点，求证：
| OA |
| OB |
（温馨提示：
| a |
| b |
| a |
| b |
分析：（1）由曲线C上的动点P到定点Q（1，0）与它到直线x+1=0的距离相等能求出曲线C的方程．
（2）设l：y=k（x-1）代入y2=4x得kx2-（2k2+4）x+k2=0．由此能够证明
•
为定值．
（2）设l：y=k（x-1）代入y2=4x得kx2-（2k2+4）x+k2=0．由此能够证明
| OA |
| OB |
解答：解：分（1）∵曲线C上的动点P到定点Q（1，0）与它到直线x+1=0的距离相等，
∴曲线C的方程是y2=4x…4分
（2）设l：y=k（x-1），
代入y2=4x，
得kx2-（2k2+4）x+k2=0…6分
设A（x1，y1）B（x2，y2），
则x1+x2=2+
，x1x2=1，
∴
•
=x1x2+y1y2=(k2+1)x1x2-k2(x1+x2)+k2=-3…9分
当l斜率不存在时，也成立∴
•
=-3．…10分
∴曲线C的方程是y2=4x…4分
（2）设l：y=k（x-1），
代入y2=4x，
得kx2-（2k2+4）x+k2=0…6分
设A（x1，y1）B（x2，y2），
则x1+x2=2+
| 4 |
| k2 |
∴
| OA |
| OB |
当l斜率不存在时，也成立∴
| OA |
| OB |
点评：本题考查直线与圆锥曲线的综合运用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为
)的直线与曲线C交于A，B两点，线段AB的垂直平分线m交x轴于点P，证明：|FP|－|FP|·cos2α为定值，并求出此定值．
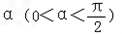的直线与曲线C交于A，B两点，线段AB的垂直平分线m交x轴于点P，证明：|FP|﹣|FP|·cos2α为定值，并求出此定值