题目内容
已知曲线C上的动点P到点F(2,0)的距离比它到直线x=﹣1的距离大1.
(I)求曲线C的方程;
(II)过点F(2,0)且倾斜角为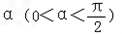 的直线与曲线C交于A,B两点,线段AB的垂直平分线m交x轴于点P,证明:|FP|﹣|FP|·cos2α为定值,并求出此定值
的直线与曲线C交于A,B两点,线段AB的垂直平分线m交x轴于点P,证明:|FP|﹣|FP|·cos2α为定值,并求出此定值
(I)解:设动点P(x,y),动点P到点F(2,0)的距离比它到直线x=﹣1的距离多1,
即动点P到点F(2,0)的距离等于它到直线x=﹣2的距离
∴ 两边平方(x﹣2)2+y2=(x+2)2
两边平方(x﹣2)2+y2=(x+2)2
化简可得:y2=8x
(II)证明:如图,作AC⊥l,BD⊥l,
设A,B的横坐标分别为xA,xB
则 =|FA|cosα+4,解得
=|FA|cosα+4,解得
同理|FB|=4﹣|FB|cosα,解得
记m与AB的交点为E,
则|FE|=|FA|﹣|AE|= =
= =
=
∴
故
即FP|﹣|FP|cos2α为定值,定值为8.
即动点P到点F(2,0)的距离等于它到直线x=﹣2的距离
∴
 两边平方(x﹣2)2+y2=(x+2)2
两边平方(x﹣2)2+y2=(x+2)2化简可得:y2=8x
(II)证明:如图,作AC⊥l,BD⊥l,
设A,B的横坐标分别为xA,xB
则
 =|FA|cosα+4,解得
=|FA|cosα+4,解得
同理|FB|=4﹣|FB|cosα,解得

记m与AB的交点为E,
则|FE|=|FA|﹣|AE|=
 =
= =
=
∴

故

即FP|﹣|FP|cos2α为定值,定值为8.


练习册系列答案
相关题目