题目内容
已知f(x)=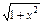 ,a≠b,
,a≠b,
求证:|f(a)-f(b)|<|a-b|.
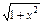 ,a≠b,
,a≠b,求证:|f(a)-f(b)|<|a-b|.
证明略
方法一 ∵f(a)= ,f(b)=
,f(b)=  ,
,
∴原不等式化为| -
- |<|a-b|.
|<|a-b|.
∵| -
- |≥0,|a-b|≥0,
|≥0,|a-b|≥0,
∴要证| -
- |<|a-b|成立,
|<|a-b|成立,
只需证( -
- )2<(a-b)2.
)2<(a-b)2.
即证1+a2+1+b2-2
 <a2-2ab+b2,
<a2-2ab+b2,
即证2+a2+b2-2
 <a2-2ab+b2.
<a2-2ab+b2.
只需证2+2ab<2
 ,
,
即证1+ab<
 .
.
当1+ab<0时,∵
 >0,
>0,
∴不等式1+ab<
 成立.
成立.
从而原不等式成立.
当1+ab≥0时,要证1+ab<
 ,
,
只需证(1+ab)2<(
 )2,
)2,
即证1+2ab+a2b2<1+a2+b2+a2b2,即证2ab<a2+b2.
∵a≠b,∴不等式2ab<a2+b2成立.∴原不等式成立.
方法二 ∵|f(a)-f(b)|=| -
- |
|
= =
= ,
,
又∵|a+b|≤|a|+|b|= +
+ <
< +
+ ,
,
∴ <1.
<1.
∵a≠b,∴|a-b|>0.∴|f(a)-f(b)|<|a-b|.
 ,f(b)=
,f(b)=  ,
,∴原不等式化为|
 -
- |<|a-b|.
|<|a-b|.∵|
 -
- |≥0,|a-b|≥0,
|≥0,|a-b|≥0,∴要证|
 -
- |<|a-b|成立,
|<|a-b|成立,只需证(
 -
- )2<(a-b)2.
)2<(a-b)2.即证1+a2+1+b2-2

 <a2-2ab+b2,
<a2-2ab+b2,即证2+a2+b2-2

 <a2-2ab+b2.
<a2-2ab+b2.只需证2+2ab<2

 ,
,即证1+ab<

 .
.当1+ab<0时,∵

 >0,
>0,∴不等式1+ab<

 成立.
成立.从而原不等式成立.
当1+ab≥0时,要证1+ab<

 ,
,只需证(1+ab)2<(

 )2,
)2,即证1+2ab+a2b2<1+a2+b2+a2b2,即证2ab<a2+b2.
∵a≠b,∴不等式2ab<a2+b2成立.∴原不等式成立.
方法二 ∵|f(a)-f(b)|=|
 -
- |
|=
 =
= ,
,又∵|a+b|≤|a|+|b|=
 +
+ <
< +
+ ,
,∴
 <1.
<1.∵a≠b,∴|a-b|>0.∴|f(a)-f(b)|<|a-b|.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
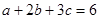 ,求证:
,求证: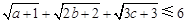 .
. ,且
,且 ,求证:
,求证:
 ≥9;
≥9; ≥
≥ .
. ,求证:
,求证: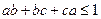 .
. .
.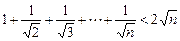 (n∈N*)
(n∈N*)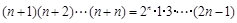 ,从
,从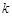 到
到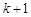 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()



 abc(a+b+c)
abc(a+b+c)