题目内容
定义数列{an}:a1=1,当n≥2时,an=
|
(Ⅰ)若当r=0时,Sn=a1+a2+…+an;
(1)求:Sn;
(2)求证:数列{S2n}中任意三项均不能构成等差数列;
(Ⅱ)求证:对一切n∈N*及r≥0,不等式
| n |
 |
| k=1 |
| 2k |
| a2k-1a2k |
分析:(1)先计算数列的前8项猜想数列的特点,数列{a2k-1}、{a2k}(k∈N*)均为等比数列,从而利用等比数列的求和公式求解即可;对于否定性的结论的证明,往往利用反证法证明;
(1)欲证此不等式
<4恒成立,先对左边式子利用拆项法求和,后再进行放缩即得.
(1)欲证此不等式
| n |
 |
| k=1 |
| 2k |
| a2k-1a2k |
解答:解:(1)当r=0时,计算得数列的前8项为:1,1,2,2,4,4,8,8.
从而猜出数列{a2k-1}、{a2k}(k∈N*)均为等比数列. (2分)
∵a2k=a2k-1=2a2k-2,a2k+1=2a2k=2a2k-1,
∴数列{a2k-1}、{a2k}(k∈N*)均为等比数列,∴a2k-1=a2k=2k-1. (4分)
①∴S2k=2(a1+a3+a5++a2k-1)=2(2k-1)=2k+1-2,S2k-1=S2k-2+a2k-1=2k-2+2k-1=3×2k-1-2,
∴Sn=
k∈N*.(6分)
②证明(反证法):假设存在三项
Sm,Sn,Sp(m,n,p∈N*,m<n<p)是等差数列,
即2Sn=Sm+Sp成立.
因m,n,p均为偶数,
设m=2m1,n=2n1,p=2p1,(m1,n1,p1∈N*),
∴2×2(2n1-1)=2(2m1-1)+2(2p1-1),
即2×2n1=2m1+2p1,
∴2n1-m1+1=1+2p1-m1,
而此等式左边为偶数,右边为奇数,这就矛盾;(10分)
(2)∵a2k=a2k-1+r=2a2k-2+r,
∴a2k+r=2(a2k-2+r),∴{a2k+r}是首项为1+2r,
公比为2的等比数列,∴a2k+r=(1+2r)•2k-1.
又∵a2k+1=2a2k=2(a2k-1+r),∴a2k+1+2r=2(a2k-1+2r),
∴{a2k-1+2r}是首项为1+2r,公比为2的等比数列,
∴a2k-1+2r=(1+2r)•2k-1. (12分)
∴
=
=
=
•[
-
],
∴
=
[
-
]
=
[
-
]<
•
=
.
∵r≥0,∴
≤4.
∴
<4. (16分)
从而猜出数列{a2k-1}、{a2k}(k∈N*)均为等比数列. (2分)
∵a2k=a2k-1=2a2k-2,a2k+1=2a2k=2a2k-1,
∴数列{a2k-1}、{a2k}(k∈N*)均为等比数列,∴a2k-1=a2k=2k-1. (4分)
①∴S2k=2(a1+a3+a5++a2k-1)=2(2k-1)=2k+1-2,S2k-1=S2k-2+a2k-1=2k-2+2k-1=3×2k-1-2,
∴Sn=
|
②证明(反证法):假设存在三项
Sm,Sn,Sp(m,n,p∈N*,m<n<p)是等差数列,
即2Sn=Sm+Sp成立.
因m,n,p均为偶数,
设m=2m1,n=2n1,p=2p1,(m1,n1,p1∈N*),
∴2×2(2n1-1)=2(2m1-1)+2(2p1-1),
即2×2n1=2m1+2p1,
∴2n1-m1+1=1+2p1-m1,
而此等式左边为偶数,右边为奇数,这就矛盾;(10分)
(2)∵a2k=a2k-1+r=2a2k-2+r,
∴a2k+r=2(a2k-2+r),∴{a2k+r}是首项为1+2r,
公比为2的等比数列,∴a2k+r=(1+2r)•2k-1.
又∵a2k+1=2a2k=2(a2k-1+r),∴a2k+1+2r=2(a2k-1+2r),
∴{a2k-1+2r}是首项为1+2r,公比为2的等比数列,
∴a2k-1+2r=(1+2r)•2k-1. (12分)
∴
| 2k |
| a2k-1a2k |
| 2k |
| [(1+2r)•2k-1-2r]•[(1+2r)•2k-1-r] |
=
| 2k-1 |
| [(1+2r)•2k-2-r]•[(1+2r)•2k-1-r] |
=
| 2 |
| 1+2r |
| 1 |
| (1+2r)•2k-2-r |
| 1 |
| (1+2r)•2k-1-r |
∴
| n |
 |
| k=1 |
| 2k |
| a2k-1a2k |
| 2 |
| 1+2r |
| n |
 |
| k=1 |
| 1 |
| (1+2r)•2k-2-r |
| 1 |
| (1+2r)•2k-1-r |
=
| 2 |
| 1+2r |
| 1 |
| (1+2r)•2-1-r |
| 1 |
| (1+2r)•2n-1-r |
| 2 |
| 1+2r |
| 2 |
| 1+2r-2r |
| 4 |
| 1+2r |
∵r≥0,∴
| 4 |
| 1+2r |
∴
| n |
 |
| k=1 |
| 2k |
| a2k-1a2k |
点评:本题主要考查了等差数列、等比数列、不等式证明中的反证法与放缩法以及数列的求和,是一道综合性很强的题目,属于难题.

练习册系列答案
相关题目
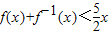 ,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).
,定义数列{an},a=8,a1=10,an=f(an-1)(n∈N*).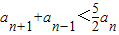 (n∈N*).
(n∈N*).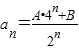 ;
;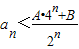 .如果存在,求出A,B的值,如果不存在,说明理由.
.如果存在,求出A,B的值,如果不存在,说明理由. ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,…. ;
;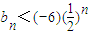 (n∈N*);
(n∈N*); 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有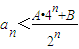 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.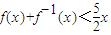 ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….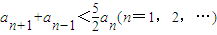 ;
;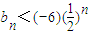 (n∈N*);
(n∈N*);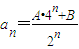 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有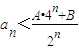 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.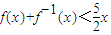 ,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….
,定义数列an:a=8,a1=10,an=f(an-1),n=1,2,….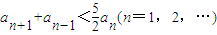 ;
;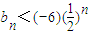 (n∈N*);
(n∈N*);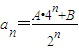 成立;②当n=2,3,…时,有
成立;②当n=2,3,…时,有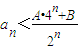 成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.
成立.如果存在满足上述条件的实数A、B,求出A、B的值;如果不存在,证明你的结论.