��Ŀ����
�躯��f��x���Ķ�����ֵ���ΪR��f��x���ķ�����Ϊf-1��x�����Ҷ�����ʵ��x������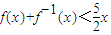 ����������an��a=8��a1=10��an=f��an-1����n=1��2������
����������an��a=8��a1=10��an=f��an-1����n=1��2��������1����֤��
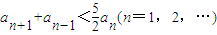 ��
����2����bn=an+1-2an��n=0��1��2��������֤��
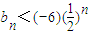 ��n��N*����
��n��N*������3���Ƿ���ڳ���A��B��ͬʱ����ٵ�n=0��n=1ʱ����
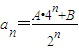 �������ڵ�n=2��3����ʱ����
�������ڵ�n=2��3����ʱ����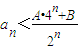 ���������������������������ʵ��A��B�����A��B��ֵ����������ڣ�֤����Ľ��ۣ�
���������������������������ʵ��A��B�����A��B��ֵ����������ڣ�֤����Ľ��ۣ�
���𰸡���������1������֪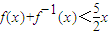 �У���x=an�����ú�������������ֵ֪ʶ������an=f��an-1����f-1��an��=an-1��������������֤�ã�
�У���x=an�����ú�������������ֵ֪ʶ������an=f��an-1����f-1��an��=an-1��������������֤�ã�
��2������1�����ι��죬�ó�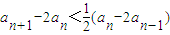 ������
������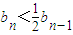 ��n��N*�����������Ƽ���֤�ã�
��n��N*�����������Ƽ���֤�ã�
��3�����ɢٽ��A=B=4��������ѧ���ɷ�֤��������ͬʱ����������ڣ���A=B=4�������ڣ�
����⣺��1����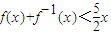 ����x=an����
����x=an����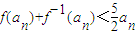 ��
��
��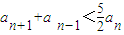 ��
��
��2����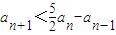 ����
����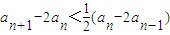 ��
��
��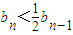 ����b=a1-2a=-6��
����b=a1-2a=-6��
��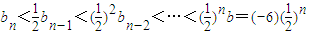 ��n��N*����
��n��N*����
��3���ɣ�2����֪��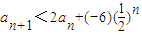 ��
��
������ڳ���A��B��ʹ��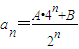 ��n=0��1������
��n=0��1������
��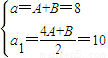 �����A=B=4��
�����A=B=4��
��������ѧ���ɷ�֤��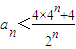 ��һ��n��2��n��N������
��һ��n��2��n��N������
1°��n=2ʱ����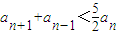 ����
����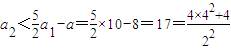 ��
��
��n=2ʱ��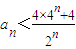 ������
������
2°����n=k��k��2��������ʽ��������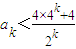 ��
��
��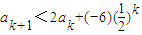
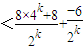 =
=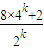 =
=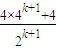
����˵��n=k+1ʱ������ʽҲ������
���Դ���A��B����A=B=4��
���������⿼�鷴�����ĸ������ʽ��֤������ѧ���ɷ���Ӧ�ã��������ת�����졢�������������������������������������⣮
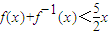 �У���x=an�����ú�������������ֵ֪ʶ������an=f��an-1����f-1��an��=an-1��������������֤�ã�
�У���x=an�����ú�������������ֵ֪ʶ������an=f��an-1����f-1��an��=an-1��������������֤�ã���2������1�����ι��죬�ó�
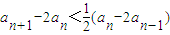 ������
������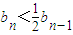 ��n��N*�����������Ƽ���֤�ã�
��n��N*�����������Ƽ���֤�ã���3�����ɢٽ��A=B=4��������ѧ���ɷ�֤��������ͬʱ����������ڣ���A=B=4�������ڣ�
����⣺��1����
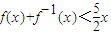 ����x=an����
����x=an����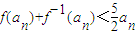 ��
����
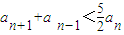 ��
����2����
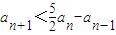 ����
����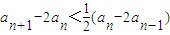 ��
����
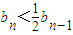 ����b=a1-2a=-6��
����b=a1-2a=-6����
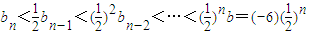 ��n��N*����
��n��N*������3���ɣ�2����֪��
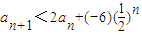 ��
��������ڳ���A��B��ʹ��
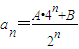 ��n=0��1������
��n=0��1��������
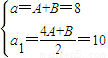 �����A=B=4��
�����A=B=4����������ѧ���ɷ�֤��
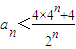 ��һ��n��2��n��N������
��һ��n��2��n��N������1°��n=2ʱ����
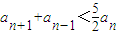 ����
����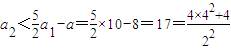 ��
����n=2ʱ��
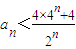 ������
������2°����n=k��k��2��������ʽ��������
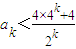 ��
����
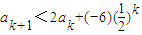
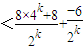 =
=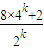 =
=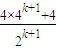
����˵��n=k+1ʱ������ʽҲ������
���Դ���A��B����A=B=4��
���������⿼�鷴�����ĸ������ʽ��֤������ѧ���ɷ���Ӧ�ã��������ת�����졢�������������������������������������⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ����b=f��
����b=f�� ���Ĵ�С��ϵΪ________��
���Ĵ�С��ϵΪ________�� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ ��
���Ĵ�С��ϵΪ �� ����b=f��
����b=f�� ���Ĵ�С��ϵΪ�� ����
���Ĵ�С��ϵΪ�� ����