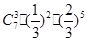题目内容
口袋里放有大小相同的2个红球和1个白球,有放回的每次摸取一个球,定义数列{an}:an=
,如果Sn为数列{an}的前n项之和,那么S7=3的概率为( )
|
分析:S7=3说明共摸球七次,只有两次摸到红球,由于每次摸球的结果数之间没有影响,故可以用独立事件的概率乘法公式求解.
解答:解:由题意S7=3说明共摸球七次,只有两次摸到红球,
因为每次摸球的结果数之间没有影响,摸到红球的概率是
,摸到白球的概率是
所以只有两次摸到红球的概率是
(
)5(
)2=
故选B
因为每次摸球的结果数之间没有影响,摸到红球的概率是
| 2 |
| 3 |
| 1 |
| 3 |
所以只有两次摸到红球的概率是
| C | 2 7 |
| 1 |
| 3 |
| 2 |
| 3 |
| 28 |
| 729 |
故选B
点评:本题考查独立事件的概率乘法公式,考查学生分析解决问题的能力,确定S7=3说明共摸球七次,只有两次摸到红球是关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
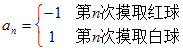 . 如果
. 如果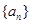 :
: ,如果
,如果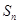 是数列
是数列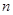 项和,那么
项和,那么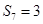 的概率是( )
的概率是( ) 、
、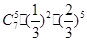
 、
、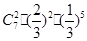
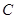 、
、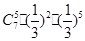
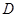 、
、
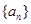 :
: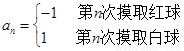 ,如果
,如果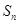 是数列
是数列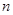 项和,那么
项和,那么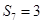 的概率是(
)
的概率是(
)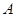 、
、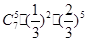
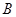 、
、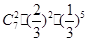
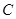 、
、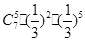
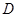 、
、