题目内容
 如图,α⊥β,α∩β=l,A∈α,B∈β,点A在直线l 上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=
如图,α⊥β,α∩β=l,A∈α,B∈β,点A在直线l 上的射影为A1,点B在l的射影为B1,已知AB=2,AA1=1,BB1=| 2 |
(Ⅰ) 直线AB分别与平面α,β所成角的大小;
(Ⅱ)二面角A1-AB-B1的余弦值.
分析:(Ⅰ) 根据面面垂直的性质定理,可知BB1⊥α.AA1⊥β,直线AB分别与平面α,β所成角分别为∠BAB1,∠ABA1,解相关的三角形即可.
(Ⅱ)在平面α内过A1作A1E⊥AB1交AB1于E,证出A1E⊥平面AB1B,再过E作EF⊥AB交AB于F,连接A1F,则∠A1FE 为所求角.解三角形A1FE即可.
(Ⅱ)在平面α内过A1作A1E⊥AB1交AB1于E,证出A1E⊥平面AB1B,再过E作EF⊥AB交AB于F,连接A1F,则∠A1FE 为所求角.解三角形A1FE即可.
解答: 解:(Ⅰ)如图,连接A1B,AB1,∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,
解:(Ⅰ)如图,连接A1B,AB1,∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,
∴AA1⊥β,BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中,BB1=
,AB=2,∴sin∠BAB1=
=
.∴∠BAB1=45°.
Rt△AA1B中,AA1=1,AB=2,sin∠ABA1=
=
,∴∠ABA1=30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ)∵BB1⊥α,∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,
则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=
.∴Rt△AA1B中,A1B=
=
=
. 由AA1•A1B=A1F•AB得 A1F=
=
=
,
∴在Rt△A1EF中,sin∠A1FE=
=
,∴二面角A1-AB-B1的余弦值是
,
 解:(Ⅰ)如图,连接A1B,AB1,∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,
解:(Ⅰ)如图,连接A1B,AB1,∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l,∴AA1⊥β,BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中,BB1=
| 2 |
| BB1 |
| AB |
| ||
| 2 |
Rt△AA1B中,AA1=1,AB=2,sin∠ABA1=
| AA1 |
| AB |
| 1 |
| 2 |
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ)∵BB1⊥α,∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,
则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=
| 2 |
| AB2-AA12 |
| 4-1 |
| 3 |
| AA1•A1B |
| AB |
1×
| ||
| 2 |
| ||
| 2 |
∴在Rt△A1EF中,sin∠A1FE=
| A1E |
| A1F |
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查空间角的计算,线面垂直,面面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
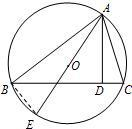
 9、如图所示的程序框图的输出结果为( )
9、如图所示的程序框图的输出结果为( )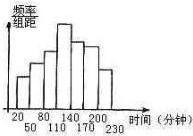
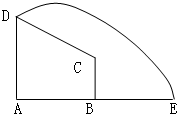 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4, 5、执行如图所示的程序框图,输出的T=
5、执行如图所示的程序框图,输出的T=