题目内容
已知单调递增的等比数列{an}满足a1+a2+a3=14,且a2+1是a1,a3的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an,求数列{bn}的前n项和Sn;
(3)若存在n∈N*,使得Sn+1﹣2≤8n3λ成立,求实数λ的最小值.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:
解题思路:(1)设出等比数列的首项与公比,列出关于 的方程组,解得即可;(2)由(1)得出
的方程组,解得即可;(2)由(1)得出 ,利用错位相减法求和;(3)先进行变量分离,转化为求关于
,利用错位相减法求和;(3)先进行变量分离,转化为求关于 的函数的最值问题.
的函数的最值问题.
规律总结:涉及等差数列或等比数列的通项问题,往往列出关于基本量的方程组,进而求出基本量,数列求和的方法主要有:倒序相加法、裂项抵消法、分组求和法、错位相减法.
注意点:存在n∈N*,使得 成立,只需
成立,只需 ,而不是最大值.
,而不是最大值.
试题解析:(1)设等比数列 的公比为q,
的公比为q,
∵a1+a2+a3=14,且a2+1是a1,a3的等差中项,
∴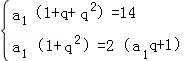 ,
,
解得q=2,a1=2,或q= ,a1=8(舍)
,a1=8(舍)
∴an=2n.
(2)bn=anlog2an=n•2n,
∴ ,①
,①
2Sn=1×22+2×23+3×24+…+n×2n+1,②
①﹣②,得
= ,
,
∴ .
.
(3)由(2)知 ,
,
原问题等价于:存在n∈N*,使得 成立,
成立,
令f(n)= ,只需λ≥f(n)min即可,
,只需λ≥f(n)min即可,
∵f(n+1)﹣f(n)= =
= ,
,
∴f(n+1)﹣f(n)的正负取决于n2﹣2n﹣1=(n﹣1)2﹣2的正负,
∴f(1)>f(2)>f(3),f(3)<f(4)<…
∴f(n)min=f(3)= ,即
,即 ,
,
∴λ的最小值是 ..
..
考点:1.数列的通项公式;2.数列的前 项和.
项和.

某地今年年初有居民住房面积为 m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
(1)如果10年后该地区的人均住房面积正好比目前翻一番,那么每年应拆除的旧住房面积x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的旧房?
下列数据供计算时参考:
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
 是等比数列
是等比数列 的前
的前 项和,对于任意正整数
项和,对于任意正整数 ,则等比数列
,则等比数列 的取值范围为
的取值范围为  中,
中, ,
, ,求
,求 和
和 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 N,都有
N,都有
 为常数,且
为常数,且 .
. 与
与 函数关系为
函数关系为 ,数列
,数列 满足
满足 ,点
,点 落在
落在  ,
, 的通项公式;
的通项公式; 的前
的前 ,使
,使 恒成立时,求
恒成立时,求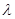 的最小值.[
的最小值.[ 的前
的前 项和为
项和为 满足
满足 (
(  )
) 为等比数列;
为等比数列; ,求数列
,求数列 的前
的前
 中,
中, 是方程
是方程 的两个根,则
的两个根,则 ____;
____;