题目内容
如图K436所示,在四棱锥P ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明:AD⊥平面PAC;
(2)求直线AM与平面ABCD所成角的正切值.

图K436
解:(1)证明:因为∠ADC=45°,且AD=AC=1,
所以∠DAC=90°,即AD⊥AC.
又PO⊥平面ABCD,AD⊂平面ABCD,
所以PO⊥AD,而AC∩PO=O,
所以AD⊥平面PAC.
(2)连接DO,取DO的中点N,连接MN,AN.
因为M为PD的中点,所以MN∥PO,
且MN= PO=1.
PO=1.
由PO⊥平面ABCD,得MN⊥平面ABCD,
所以∠MAN是直线AM与平面ABCD所成的角.
在Rt△DAO中,AD=1,AO= ,
,
所以DO= ,从而AN=
,从而AN= DO=
DO= .
.
在Rt△ANM中,tan∠MAN= =
= =
= ,
,
即直线AM与平面ABCD所成角的正切值为 .
.

练习册系列答案
相关题目

 点M在OA上,且OM=2MA,N为BC的中点,则
点M在OA上,且OM=2MA,N为BC的中点,则 等于( )
等于( )
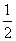 a-
a- b+
b+ 两两之间的夹角均为60°,且|
两两之间的夹角均为60°,且| |=1,
|=1, 则|
则| |等于( )
|等于( ) B.
B.
 D.
D.
 ,
, ,
, .
. 与
与 的大小;
的大小; .
.