题目内容
已知数列{Pn}满足:(1)P1=| 2 |
| 3 |
| 7 |
| 9 |
| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)设bn=Pn+1-Pn,证明数列{bn}是等比数列;
(Ⅱ)求
| lim |
| n→∞ |
分析:(Ⅰ)对Pn+2=
Pn+1+
Pn进而变形Pn+2-Pn+1=-
Pn+1+
Pn,进而可证明{Pn+1-Pn}为等比数列,即数列{bn}是等比数列
(Ⅱ)由(Ⅰ)可求得数列{bn}的通项公式,即数列{Pn+1-Pn}的通项公式,进而利用分组法,进行求和得Pn=
+
•(-
)n,进而可求得
Pn.
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)由(Ⅰ)可求得数列{bn}的通项公式,即数列{Pn+1-Pn}的通项公式,进而利用分组法,进行求和得Pn=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| lim |
| n→∞ |
解答:解:(Ⅰ)bn+1=Pn+2-Pn+1=-
Pn+1+
Pn=-
bn,
又b1=
,
∴数列{bn}是等比数列.
(Ⅱ)由(Ⅰ)知bn=
(-
)n-1=(-
)n+1,
即Pn+1-Pn=bn=(-
)n+1,
∴Pn=P1+(P2-P1)+(P3-P2)+…+(Pn-Pn-1)=
+(-
)2+(-
)3++(-
)n=
+
•(-
)n.
∴
Pn=
[
+
•(-
)n]=
.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
又b1=
| 1 |
| 9 |
∴数列{bn}是等比数列.
(Ⅱ)由(Ⅰ)知bn=
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 3 |
即Pn+1-Pn=bn=(-
| 1 |
| 3 |
∴Pn=P1+(P2-P1)+(P3-P2)+…+(Pn-Pn-1)=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题主要考查了等比数列的性质.属基础题.

练习册系列答案
相关题目
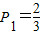 ,
,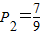 ;(2)
;(2)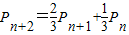 .
.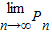 .
.