题目内容
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
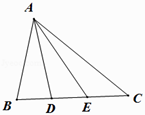
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ![]() ,求AD的长.
,求AD的长.
【答案】解:(Ⅰ)B=60°,c=4,b=6, 在△ABC中,由正弦定理 ![]() ,
,
得 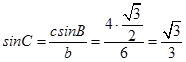 ,
,
又b>c,所以B>C,则C为锐角,所以 ![]() ,
,
则sinA=sin(B+C)=sinBcosC+cosBsinC= ![]() ,
,
所以△ABC的面积 ![]() .
.
(Ⅱ)设BD=x,则BE=2x, ![]() ,又B=60°,c=4,
,又B=60°,c=4,
在△ABE中,由余弦定理得12x2=16+4x2﹣242xcos60°,
即8x2=16﹣8x,解得x=1,
则BE=2,所以∠AEB=90°,
在直角△ADE中, ![]() .
.
【解析】(Ⅰ)根据正弦定理和两角和的正弦公式和三角形的面积公式即可求出,(Ⅱ)设BD=x,由余弦定理求出x的值,再根据勾股定理即可求出.

练习册系列答案
相关题目